daveed
- 138
- 0
SO.
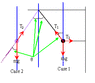
a ball is suspended by a string from the ceiling, and held at angle theta to the vertical by another string that is attached to the wall nearby... the string attched to the wall is cut and the ball swings like a pendulum, at the farthest it is theta from the vertical on both sides.
so. the book asks what is the ratio of the tension in the rope holding the rope to the ceiling before the other rope(attached to the wall) was cut, to when the ball is swinging and is at its farthest from the vertical(forming angle theta to it)
i thought it should be one to one, because the tension*sin(theta) would be supporting the ball in both cases, but it turns out the answer is cos^2(theta)
any ideas why?
a ball is suspended by a string from the ceiling, and held at angle theta to the vertical by another string that is attached to the wall nearby... the string attched to the wall is cut and the ball swings like a pendulum, at the farthest it is theta from the vertical on both sides.
so. the book asks what is the ratio of the tension in the rope holding the rope to the ceiling before the other rope(attached to the wall) was cut, to when the ball is swinging and is at its farthest from the vertical(forming angle theta to it)
i thought it should be one to one, because the tension*sin(theta) would be supporting the ball in both cases, but it turns out the answer is cos^2(theta)
any ideas why?