Why does my integrator pole disappear when I simplify this?

[CoolDude420]

Homework Statement

I have a 2nd order low-pass filter (expected to be driven by a current source) that I know has an integrator pole, a LHP pole and a LHP zero.

I need to find the location of these which I am doing by trying to find the impedance of this circuit.

Relevant Equations

n/a

I have tried two attempts at this and the strange this is - depending on where and how I apply my algebraic simplification (multiplying by s/s), I get a different answer. In attempt 1, I lose the integrator s=0 pole some how but in attempt 2, it's all fine.

Attempt 1

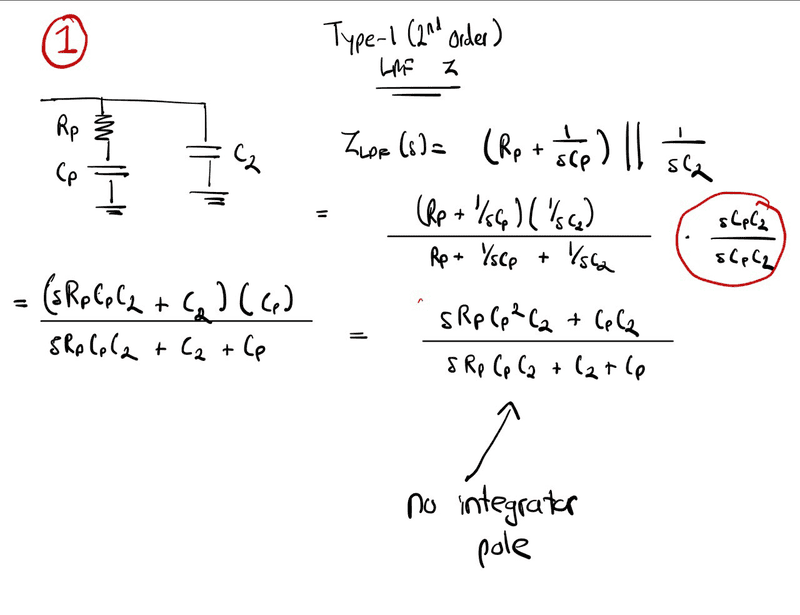
Attempt 2

PS: I have not completed this, my question is purely regarding why does the integrator pole dissapear.

So, why does the integrator pole in attempt 1 disappear but not in attempt 2?? I am really confused!

 

[anuttarasammyak]

BLUE BOX should be
R_\rho C_\rho +1/s
which makes attempts 1 and 2 have same result.

 

[CoolDude420]

View attachment 344193
BLUE BOX should be
R_\rho C_\rho +1/s
which makes attempts 1 and 2 have same result.

Oops. Can't believe I did that even though I reviewed my work 3 times! I was going crazy!
Thank you.

 

[CoolDude420]

View attachment 344193
BLUE BOX should be
R_\rho C_\rho +1/s
which makes attempts 1 and 2 have same result.

A follow up question - does it matter when I equate the denominator to 0 to get the poles. For example, if I replaced the blue box with R_\rho C_\rho +1/s, there would a 1/s term at the top, yet the bottom would be unchanged. If I just left the 1/s term on top and equated the bottom to zero at this stage of the work, I would still lose my s = 0 pole.

Do I have to ensure that the entire function is in standard terms of 's' and no quotients before equating to zero?

 

[anuttarasammyak]

The result of attempt 2 would be written as
\frac{A}{s}+\frac{B}{s+c}
where
c=R_\rho^{-1}(C_\rho^{-1}+C_2^{-1})
You can get constants A and B by calculation. You find it sum of simple pole functions. You do not have to do this reduction in applying residue theorem. The result of attempt 2 is well enough to do it. But be cafeful in your formula so that numerator does not diverge at poles.