Why Does My Relative Density Calculation Not Yield a Numerical Value?

[Taylor_1989]

Homework Statement

A person living on a planet which has half the radius of the earth, realizes that he can throw a rock 10 times further than he can on earth.

Estimate the relative density of this planet compared to that of earth. Ignore any effect of air resistance.

Relevant Equations

$$F=\frac{Gm_1m_2}{d^2}$$

$$\rho=M*V$$

So I am a bit stuck on this question as my result using the above equations dose not give an numerical value which I assume from the question is needed.

So here my method for solving

My first thought was that if on the planet the person can throw a rock 10 time further then that it implies in any direction. So I took the vertical direction, for each planet which is demonstrated by my diagram below.

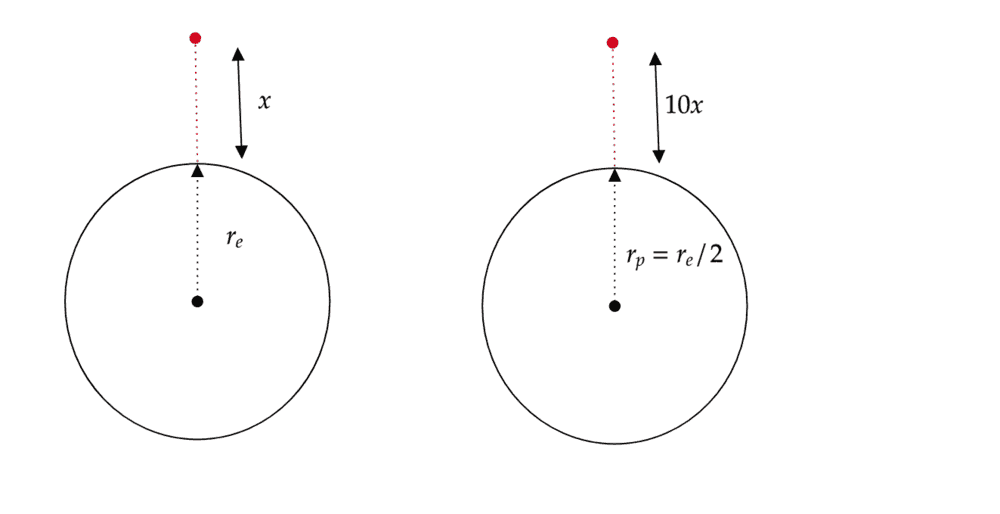
The I used Newtons law of gravity to calculate the gravity on each planet like so.

$$g_e=\frac{GM_e}{d^2}=\frac{GM_e}{(r_e+x)^2}$$$$g_p=\frac{GM_p}{d^2}=\frac{GM_p}{4(r_e+20x)^2}$$

I then rearranged each equation in terms of the mass for each planet.

$$M_e=\frac{g_e(r_e+x)^2}{G}$$

$$M_p=\frac{g_p4(r_p+x)^2}{G}$$

Next I calculated the density of each planet

$$\rho_e=M_e(\frac{4}{3}\pi r_e^3)$$

$$\rho_p=M_p(\frac{1}{6}\pi r_p^3)$$

The by dividing the two density's

$$\frac{\rho_p}{\rho_e}=\frac{M_p}{2M_e}$$

I then sub in my mass equation from earlier and with some manipulation I from the following

$$\frac{\rho_p}{\rho_e}=\frac{g_p(r_e+20x)^2}{8g_e(r_e+x)^2}$$

My issue is, that from the question I believe I am suppose to have some sort of numerical value but can't seem to figure a away of getting one.

Which leaves me with the question

1. What have I assumed wrong in this question, by using the method I have displayed above?

Addtional thought. I was just thinking that if I was on the Earth my distance in x would be x<<$r_e$ and the same goes for the planet 20x<<$r_e$, so could I assumen this in my equation above?

 

[haruspex]

You don't need to worry about the change in gravity during the flight of the rock. You can assume the distance is very small compared with the radius of the planet.

 

[rdishy]

I'm not sure about how to get a numerical ratio of the densities yet but will let you know if I do. If it helps though, you've used MV for density as opposed to M/V. What was your reasoning for adding the distance traveled by the rock to the radius of the planets? Thanks!

 

[Taylor_1989]

I'm not sure about how to get a numerical ratio of the densities yet but will let you know if I do. If it helps though, you've used MV for density as opposed to M/V. What was your reasoning for adding the distance traveled by the rock to the radius of the planets? Thanks!

It okay i figured it now, but thanks for the response. I did try an mark the post a solved but cannot find the button