Why Does Pulling a Cord Cause a Spool to Move Right?

[Leo Liu]

Homework Statement

:(

Relevant Equations

Rotational Motion, Work-Energy, Impulse

Hi folks! I was teaching myself rotational motion when encountered an example which states as follows:

My questions:
1. I do not understand why pulling the cord moves the rotating spool to the right. There were some discussions on stackexchange (https://physics.stackexchange.com/a/221148/231749), and someone concluded that "Case of rolling without slipping:
In that case the spool would be accelerating to the left (−x−x-direction) and the spool will be rotating anti-clockwise." Could anyone elucidate the motion in this question?

2. I do not really know how to calculate the work done by the tension. It would be great if someone can explain it.

3. I tried to find the friction by calculating the torque, but I did not get the same answer as the textbook. Is it because the torque of the tension exerted on the spool is not always perpendicular to the r?
My work:

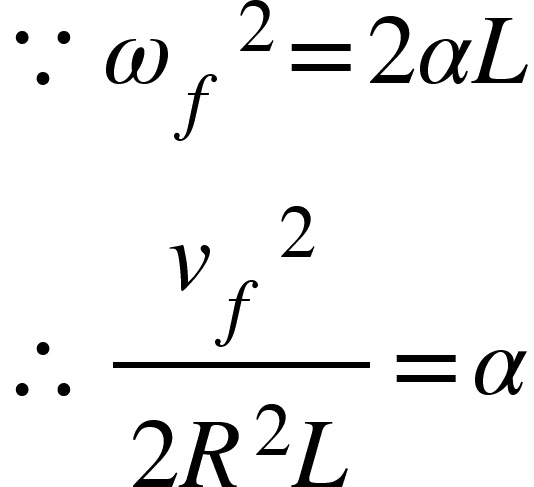
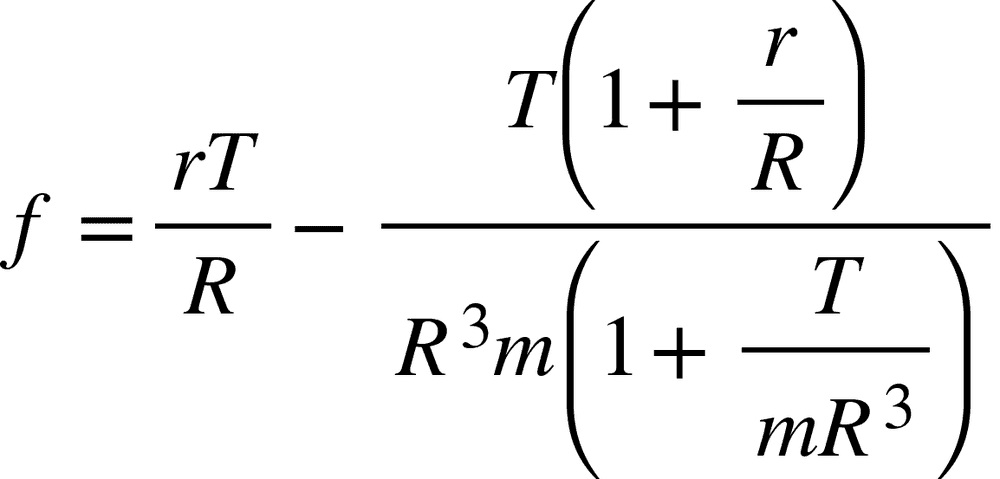
Thanks in advance and merry Christmas!

 

[rcgldr]

Did you take into account that the table's horizontal component of force exerted is also to the right?

 

[Leo Liu]

Did you take into account that the table's horizontal component of force exerted is also to the right?

Hi. Do you mean the friction?

 

[haruspex]

Hi. Do you mean the friction?

Yes, the friction could act to the right. It depends on how high the pulled string is. Impossible to say without knowing the ratios of the distances. But you do not need to care about it - the algebra is the same.

 

[haruspex]

I do not understand why pulling the cord moves the rotating spool to the right.

It seems obvious that a force to the right (the tension) would tend to move it to the right. Can you explain more what bothers you about that?

 

[haruspex]

2. I do not really know how to calculate the work done by the tension. It would be great if someone can explain it.

3. I tried to find the friction by calculating the torque, but I did not get the same answer as the textbook. Is it because the torque of the tension exerted on the spool is not always perpendicular to the r?
My work:

View attachment 254682

As the text indicates, if you can find the tension and the distance the hand moves then multiplying them will give the work done. What is the relationship between the linear velocity of the spool and that of the string?

Wrt your equations, the first one appears to be dimensionally invalid. The LHS has dimension T^-2 but the RHS LT^-2.

 

[rcgldr]

Did you take into account that the table's horizontal component of force exerted is also to the right?

Hi. Do you mean the friction?

Since the radius for the tension component is smaller than the radius of the wheel, the tension exerts a clockwise torque, and the wheels rate of rotation would accelerate at a greater rate without friction than with friction (from the tabletop). The horizontal component of force from the tabletop is to the right, in the same direction as the tension, but partially countering the torque related to tension.
Yes if the tension in the cable results in a torque that would produce greater angular acceleration if there was no friction.

 

[Leo Liu]

As the text indicates, if you can find the tension and the distance the hand moves then multiplying them will give the work done. What is the relationship between the linear velocity of the spool and that of the string?

Wrt your equations, the first one appears to be dimensionally invalid. The LHS has dimension T^-2 but the RHS LT^-2.

Could you tell me why do we need to consider the work done by the tension exerted along

? Why shouldn't it just be W = FL? Thank you.

Derivation:

(I am sorry the middle one should be 2aR instead)

 

[rcgldr]

Someone has answered this on stackexchange

That is a different case, in that case, the string is being wound around the bottom of the inner axis, while in this question, the string is being unwound from the top of the inner axis.

 

[Leo Liu]

That is a different case, in that case, the string is being wound around the bottom of the inner axis, while in this question, the string is being unwound from the top of the inner axis.

Never mind, I misinterpreted the question. Thank you!

 

[haruspex]

Yes. Since the radius for the tension component is smaller than the radius of the wheel, the tension exerts a clockwise torque, and the wheels rate of rotation would accelerate at a greater rate without friction than with friction (from the tabletop). The horizontal component of force from the tabletop is to the right, in the same direction as the tension, but partially countering the torque related to tension.

As I commented,
a) it is not possible to say which way friction will act without further information; e.g. suppose r is very small compared with R: T would exert little torque, so friction must act to the left to provide the necessary angular acceleration; alternatively, with r=R, T provides too much torque and friction acts to the right; in between there is a ratio of r to R for which there is no frictional force.
b) we do not need to worry about which way friction acts; the equations are the same.

 

[haruspex]

Why shouldn't it just be W = FL?

The work the hand does is that of pulling with a force T some distance. The hand does not know what it is pulling, only the force it exerts and the distance it moves in that direction.
But the expression you have for that distance, $\frac rRL$, implies it is less than L. Does that seem right?

Wrt "$\omega_f=\alpha\Delta x$", if I interpret those variables correctly, says a rate of rotation (dimension T^-1) equals an angular acceleration (dimension T^-2) multiplied by a displacement (dimension L). Not possible.

 

[Leo Liu]

The work the hand does is that of pulling with a force T some distance. The hand does not know what it is pulling, only the force it exerts and the distance it moves in that direction.
But the expression you have for that distance, $\frac rRL$, implies it is less than L. Does that seem right?

Wrt "$\omega_f=\alpha\Delta x$", if I interpret those variables correctly, says a rate of rotation (dimension T^-1) equals an angular acceleration (dimension T^-2) multiplied by a displacement (dimension L). Not possible.

Got it, thanks