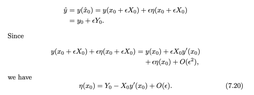SUMMARY
Taylor's Theorem utilizes the notation +O(ε) to describe the magnitude of error as ε approaches 0, emphasizing that the sign of the error can vary with ε. The expression f = g + O(ε) indicates that there exists a positive constant M such that |f - g| ≤ M|ε|. Conversely, using -O(ε) would imply a transformation to g = f + O(ε), which is mathematically equivalent. Therefore, the convention of using +O(ε) is universally accepted in mathematical literature.
PREREQUISITES
- Understanding of Taylor's Theorem
- Familiarity with Big O notation
- Basic calculus concepts, particularly limits
- Knowledge of error analysis in mathematical functions
NEXT STEPS
- Study the derivation of Taylor's Theorem in detail
- Learn about the implications of Big O notation in error analysis
- Explore the differences between +O(ε) and -O(ε) in mathematical proofs
- Investigate applications of Taylor's Theorem in numerical methods
USEFUL FOR
Mathematicians, students of calculus, and anyone involved in numerical analysis or error estimation in mathematical functions will benefit from this discussion.