- #1
Frigus
- 337
- 160
As we know that liquids(same) at same height exert same pressure because of height difference but as I have a question in which there are some figures In which the (d) part lower part is extended horizontally,so by common sense the pressure in horizontal direction should increase But why at that level(horizontal) pressure increases from all sides?
Please try to tell me verbally not by proving it mathematically.
<< Mentor Note -- Two similar threads merged into this one >>
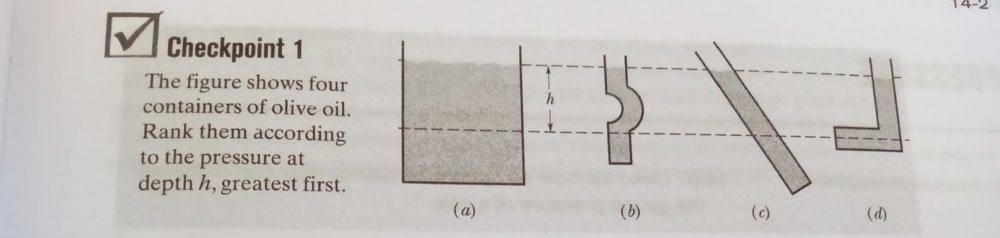
Please try to tell me verbally not by proving it mathematically.
<< Mentor Note -- Two similar threads merged into this one >>
Last edited by a moderator: