Mark44 said:
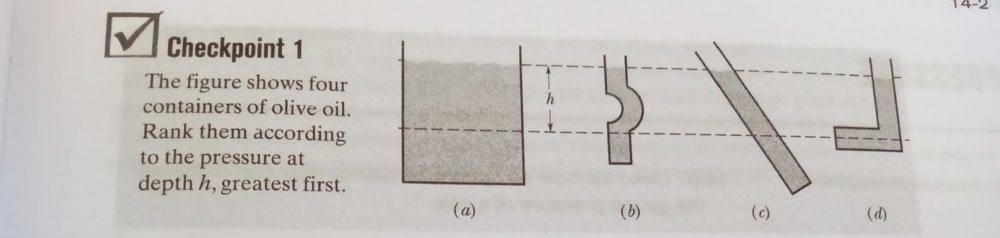
The pressure at a given depth is a function solely of the depth of the fluid. Extending the container horizontally has no effect on the pressure. In figure d, at every point on the lower dotted line the pressure is the same.
Hemant said:
I explained why in the first sentence of what I wrote way back in post #2. I have copied it to this post, with the explanation in bold.
Hemant said:
Can anyone also explain me this case,
If we create a pressure in liquid by pushing the piston in given figure a same pressure will be developed in height a and b a irrespective of their area please tell me why a same pressure propagates.
There is an important difference between the image of the four containers in post #1, and the image of the funnel shaped container in post #21.
The containers shown in post #1 are all open at the top, so the weight of the air in the atmosphere above each container is pressing down on the top layer of the liquid in the container. The pressure at the top layer of the liquid is about 14.7 lb/in^2. At lower levels in each container, there is also the additional weight of the liquid above, so the pressure is higher at lower horizontal levels (i.e., for larger values of h). For container d, with a horizontal extension, it doesn't matter how far horizontally that extension goes -- all points at the same horizontal level have the same height of fluid and the same column of atmospheric air pressing on them, so the pressure is the same at each point that is h units below the top of the liquid.
The container in post #21 is different, because it is closed at the top, so the air in the atmosphere is not pressing down on the top layer of fluid. Let's say that you start the experiment by turning the container over and filling it with fluid, and then inserting the piston so that there is no air between the piston and fluid. Now turn the container again so that the piston is at the bottom. At this time, because of atmospheric pressure on the outer end of the piston, the pressure inside the container will be the same as atmospheric pressure, about 14.7 lb/in^2.
If you push on the piston, you're squeezing the molecules of liquid near the piston. These molecules in turn push against other molecules higher up until all of the fluid in the container reaches the same, higher pressure. When you apply a force on the piston, which has a certain cross-sectional area, you're increasing the pressure on the liquid in the container, and that pressure propagates to all points, and all levels of that container. In this case, because the container is closed, it's not possible for the pressure to be greater at some places than at others.