Why is 2/3 required in the calculation for the equilibrium of rigid bodies?

[goldfish9776]

Homework Statement

why 2/3 is required in this calculation as circled ? I have no idea.
I know that 4.5/2 is the distance of the centroid of the bar from point A .

Homework Equations

The Attempt at a Solution

 

[Feodalherren]

Because it is not a constant load, the load increases as you move to the right. Do you know how to draw Shear/Moment diagrams?

 

[SteamKing]

Homework Statement

why 2/3 is required in this calculation as circled ? I have no idea.
I know that 4.5/2 is the distance of the centroid of the bar from point A .

Homework Equations

The Attempt at a Solution

The calculation shown is not about the centroid of the bar is located; it's about where the centroid of the triangular load is located from the left support.

 

[goldfish9776]

The calculation shown is not about the centroid of the bar is located; it's about where the centroid of the triangular load is located from the left support.

well , can you explain what the 2/3 means here?

 

[SteamKing]

well , can you explain what the 2/3 means here?

The centroid of a right triangle is located 2/3 of the length of the base from the pointy end.

https://en.wikipedia.org/wiki/List_of_centroids

 

[goldfish9776]

The centroid of a right triangle is located 2/3 of the length of the base from the pointy end.

https://en.wikipedia.org/wiki/List_of_centroids

2 x 4.5 is the force ... then why 1/2 appear in the calculations?

 

[SteamKing]

2 x 4.5 is the force ... then why 1/2 appear in the calculations?

Is 2 kN/m x 4.5 m total the force? Wouldn't that be true only if the 2 kN/m distributed load was applied evenly over the entire length of the beam?

 

[goldfish9776]

Is 2 kN/m x 4.5 m total the force? Wouldn't that be true only if the 2 kN/m distributed load was applied evenly over the entire length of the beam?

you mean the different points at entire length of rod have different forces? if so, why shouldn't the force = 2x4.5x2/3 ?
since the force involved only from point A to centroid ...

 

[SteamKing]

you mean the different points at entire length of rod have different forces? if so, why shouldn't the force = 2x4.5x2/3 ?
since the force involved only from point A to centroid ...

You've apparently missed some basic instruction in how distributed loads are represented. Here are two commonly encountered types of distributed loadings:

​

Unlike with a concentrated load, the individual arrows in the figures on the left do not represent individual loads; they are merely diagrammatic. The equivalent concentrated load and its location are given in the corresponding figures to the right.

The first type is the uniformly distributed load. This is a loading which has a constant amount of force applied per unit length along the beam. In the diagram, this load is w kN/m, for example.
The Total Load = w * L and its center is located at L/2 from one end of the beam.

The second type is the uniformly varying load. This is a loading which has a zero amount of force applied per unit length at the right end of the beam, and this loading increases in a linearly increasing fashion until it reaches say w kN/m at the left end of the beam.
The Total Load = (1/2)*w*L and its center is located at (2/3) of the length of the beam from the end where w = 0.

 

[goldfish9776]

You've apparently missed some basic instruction in how distributed loads are represented. Here are two commonly encountered types of distributed loadings:

​

Unlike with a concentrated load, the individual arrows in the figures on the left do not represent individual loads; they are merely diagrammatic. The equivalent concentrated load and its location are given in the corresponding figures to the right.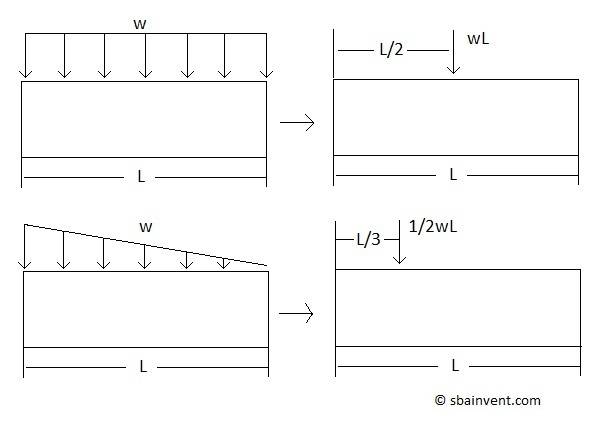

The first type is the uniformly distributed load. This is a loading which has a constant amount of force applied per unit length along the beam. In the diagram, this load is w kN/m, for example.
The Total Load = w * L and its center is located at L/2 from one end of the beam.

The second type is the uniformly varying load. This is a loading which has a zero amount of force applied per unit length at the right end of the beam, and this loading increases in a linearly increasing fashion until it reaches say w kN/m at the left end of the beam.
The Total Load = (1/2)*w*L and its center is located at (2/3) of the length of the beam from the end where w = 0.

ok , why The Total Load = (1/2)*w*L is located at (2/3) of the length of the beam from the end where w = 0.
why not w*L as in the first case ?

 

[SteamKing]

ok , why The Total Load = (1/2)*w*L is located at (2/3) of the length of the beam from the end where w = 0.
why not w*L as in the first case ?

Because most of the total load is located toward the end opposite of the end of the beam where w = 0.

If you took each beam as loaded in the diagrams, and placed a fulcrum under the location of the center of the total load, the beam would be balanced, which indicates that the moments of the load on either side of the fulcrum produce equal and opposite rotation of the beam. The moments cancel out, the rotations cancel out, and the beam is balanced around the point.

It's like playing on a see-saw: as long as the load on each end of the seesaw is the same and is located the same distance away from the middle, the see-saw is balanced. Add some more load to one side, and the see-saw wants to sink on that side.

I can't believe you've never tried to balance anything, a ruler, a stick, a bat, a baton.

 

[goldfish9776]

Because most of the total load is located toward the end opposite of the end of the beam where w = 0.

If you took each beam as loaded in the diagrams, and placed a fulcrum under the location of the center of the total load, the beam would be balanced, which indicates that the moments of the load on either side of the fulcrum produce equal and opposite rotation of the beam. The moments cancel out, the rotations cancel out, and the beam is balanced around the point.

It's like playing on a see-saw: as long as the load on each end of the seesaw is the same and is located the same distance away from the middle, the see-saw is balanced. Add some more load to one side, and the see-saw wants to sink on that side.

I can't believe you've never tried to balance anything, a ruler, a stick, a bat, a baton.

so , at the distance 2L/3 from the position where w= 0 , the force only become wL/2 ?
Is there any mathematical proof for this ? it's hard for me to fully understand it

 

[SteamKing]

so , at the distance 2L/3 from the position where w= 0 , the force only become wL/2 ?
Is there any mathematical proof for this ? it's hard for me to fully understand it

No, the total load over the entire length of the beam = wL/2.

The total load is the area under the distributed load diagram, which in this case is a triangle. What's the area of a right triangle where the base is L units long and the height is w units?

When the loading has a uniform distribution, the distributed load diagram is a rectangle of length L and height of w. What's the area of this rectangle?

Those are your mathematical proofs.