Jhenrique
- 676
- 4
The cauchy principal value formula is:
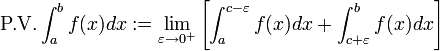
But why ε→0⁺ in both terms? The correct wouldn't be ε→0⁻ in 1st term and ε→0⁺ in 2nd term? Like:
\lim_{\varepsilon \to 0^-}\int_{a}^{c-\varepsilon}f(x)dx + \lim_{\varepsilon \to 0^+}\int_{c+\varepsilon}^{b}f(x)dx
?
But why ε→0⁺ in both terms? The correct wouldn't be ε→0⁻ in 1st term and ε→0⁺ in 2nd term? Like:
\lim_{\varepsilon \to 0^-}\int_{a}^{c-\varepsilon}f(x)dx + \lim_{\varepsilon \to 0^+}\int_{c+\varepsilon}^{b}f(x)dx
?