- #1
Happiness
- 679
- 30
Consider a rope wraps an angle ##\theta## around a pole with a coefficient of static friction ##\mu##. You pull one end with a tension ##T_0##. The force that the other end can support is given by ##T=T_0e^{\mu\theta}##(derivation below). For ##\mu=1## and ##\theta=2\pi##, ##T=530T_0##. That means with the help of static friction, you can wrap a rope one round around a pole to hold up a weight 530 times ##T_0##! Suppose I can carry a maximum weight of 50 kg tied to a rope. By wrapping the rope once around a pole, I'll be able to support ##530\times50=26500##kg! That's the weight of an aeroplane! Doesn't this sound dubious? But this is what is claimed by the book below.
Next, let's explain why force is a scalar here. The reason why the tension at the other end is ##530T_0## is because static friction is always acting in the same direction along the rope, say anticlockwise. This static friction at different parts of the rope is being summed up as a scalar to give a value of ##529T_0##. Then add this to the ##T_0## you exert, we get ##T=530T_0##.
If we treat friction as a vector instead, we will say that the friction at different parts of the rope is in different directions. When the rope is wrapped once, the vector sum of friction is zero since vectors arranged in a circle go back to the same point.
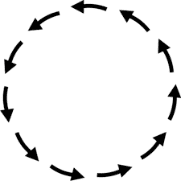
Then, we will conclude ##T=T_0##. After wrapping the rope once around a pole, the maximum weight I can support remains the same.
Which is correct? The scalar sum or the vector sum?


Next, let's explain why force is a scalar here. The reason why the tension at the other end is ##530T_0## is because static friction is always acting in the same direction along the rope, say anticlockwise. This static friction at different parts of the rope is being summed up as a scalar to give a value of ##529T_0##. Then add this to the ##T_0## you exert, we get ##T=530T_0##.
If we treat friction as a vector instead, we will say that the friction at different parts of the rope is in different directions. When the rope is wrapped once, the vector sum of friction is zero since vectors arranged in a circle go back to the same point.
Then, we will conclude ##T=T_0##. After wrapping the rope once around a pole, the maximum weight I can support remains the same.
Which is correct? The scalar sum or the vector sum?
Last edited: