dbag123
- 76
- 3
- Homework Statement
- Determine the lenght of h with respect to b so that the water flows.
- Relevant Equations
- sum of moments at the hinge
Hello
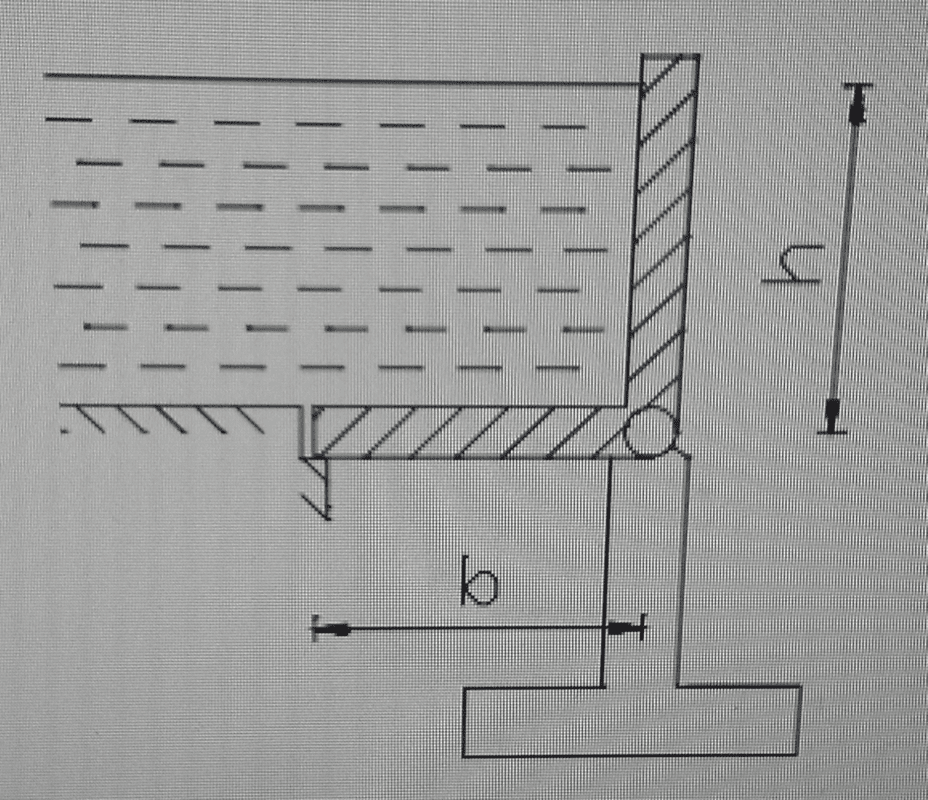
Ihave gotten as far as coming up with an equation for the sum of moments and it goes as follows: bh*1/2b-1/2hb*1/3b=0 the answer for h i get is wrong and i don't know if i am missing something. moment arm on the b is 1/2b and the moment arm on h is 1/3h because of the way water pressure works , meaning its a uniform load in the shape of triangle. bh is my way of writing the force as a point load acting on the levers. The answer to this problem is supposed to be h= √3 *b. Any help is appreciated.
Ihave gotten as far as coming up with an equation for the sum of moments and it goes as follows: bh*1/2b-1/2hb*1/3b=0 the answer for h i get is wrong and i don't know if i am missing something. moment arm on the b is 1/2b and the moment arm on h is 1/3h because of the way water pressure works , meaning its a uniform load in the shape of triangle. bh is my way of writing the force as a point load acting on the levers. The answer to this problem is supposed to be h= √3 *b. Any help is appreciated.