yonese
- 15
- 1
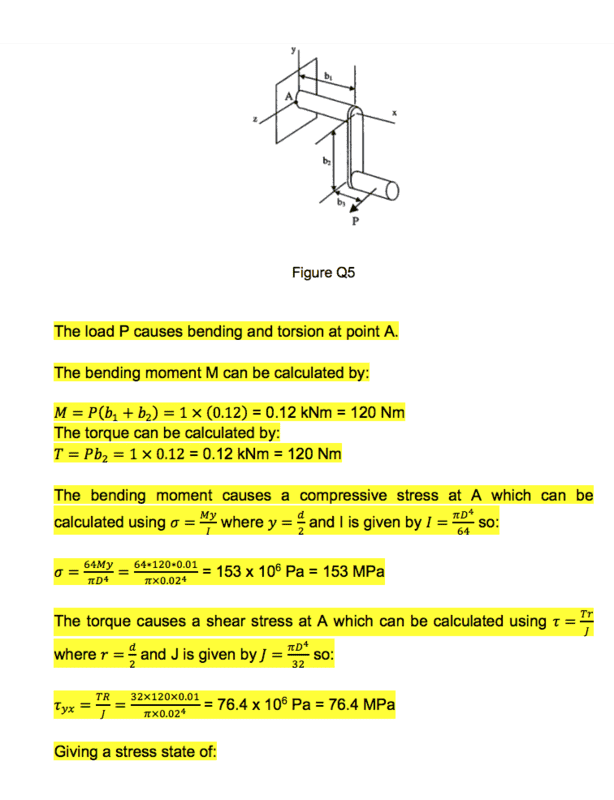
Summary:: I'm stuck on a year 2 mechanics question. I have this simplified crankshaft with a load P at the end. The solutions to the exercise have said that point A is in compression due to a bending moment but I don't understand why that is. The solutions and my calculations have both come out with positive values for the stress at A, and I thought a positive value for stress = tension, negative = compression.