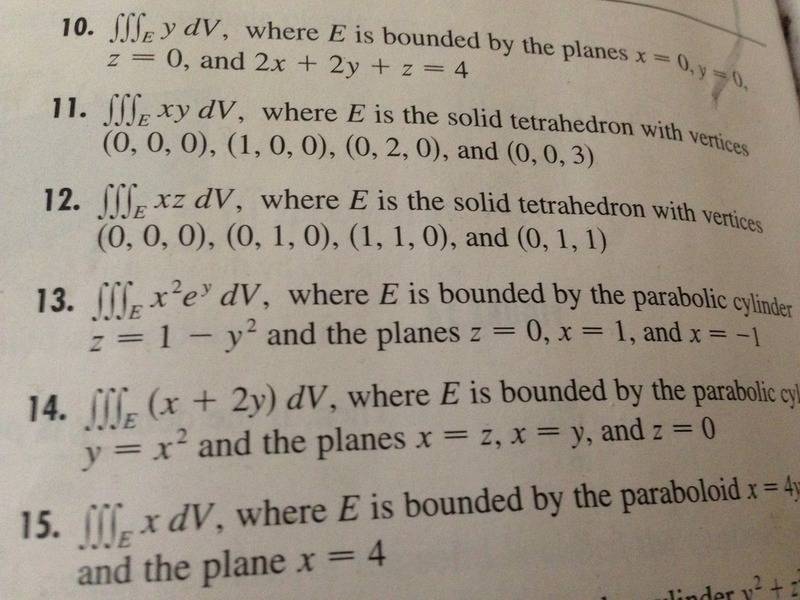namehere
- 2
- 0
Moved from a technical forum and thus no template
Here on problem #13 i am getting a false solution when only taking the volume of the region in quadrant 1 and multiplying it by 4. The later photo contains the correct solution which is obtained by taking the volume of the entire region. Can someone explain to me why the former is incorrect.