Why is the area under a curve the integral?

[dgamma3]

here is a geometric proof, similar to the one in my textbook (copied from Aryabhata, from http://math.stackexchange.com/questions/15294/why-is-the-area-under-a-curve-the-integral) :

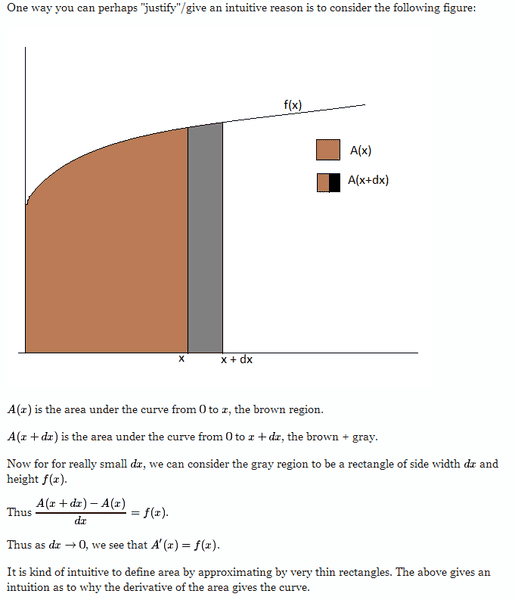
Is this saying: that the A' equals the function. Which is implying, that the integration of A equals F (where F is the integral of f)?

thanks

 

[Fredrik]

You don't prove that the integral of a function is the area under its graph. What you do is to extend the definition of the "area" (which is initially only defined for rectangles) to regions of shapes like this, by saying that the area of such a region is the integral of the function. This is just a choice to use the word "area" in these situations, nothing more. So it can't be proved.

What you can do is to explain why the word "area" was chosen for this concept.

The argument you posted says that A'=f. By the fundamental theorem of calculus, this implies that for all real numbers a,b,
$$\int_a^b f(x)dx =\int_a^b A'(x)dx =A(b)-A(a).$$

 

[Vargo]

@Fredrik
Perhaps I am being pedantic, but the fact that the integral equals area is a theorem rather than just a definition.

See the following links:
http://en.wikipedia.org/wiki/Jordan_measure
http://terrytao.files.wordpress.com/2011/01/measure-book1.pdf

In calculus, it is often treated as a definition, but the justification is basically there using lower/upper Riemann sums.

@OP
The above is just a quibble that does not have much to do with your question.

 

[Fredrik]

@Fredrik
Perhaps I am being pedantic, but the fact that the integral equals area is a theorem rather than just a definition.

If we have already defined "area" using a measure, then yes. But the OP clearly hadn't. People who ask why the integral is the area under the graph don't know what a measure is. So it makes sense to take the integral as the definition at this point.