Why Is the Exerted Force Equal and Opposite to the Electrostatic Force?

[ewr]

Hi, I found this on http://farside.ph.utexas.edu/teaching/302l/lectures/node32.html

"Consider a charge

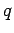placed in a uniform electric field

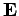(e.g., the field between two oppositely charged, parallel conducting plates). Suppose that we very slowly displace the charge by a vector displacement

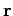in a straight-line. How much work must we perform in order to achieve this? Well, the force

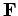we must exert on the charge is equal and opposite to the electrostatic force

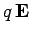experienced by the charge (i.e., we must overcome the electrostatic force on the charge before we are free to move it around). The amount of work

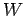we would perform in displacing the charge is simply the product of the force we exert, and the displacement of the charge in the direction of this force."

My question is why is the force we must exert on the charge is equal and opposite to the electrostatic force qE? Shouldn't the force be greater than qE? If it is equal and opposite than the charge won't move wouldn't it?

Thank you.

 

[Orodruin]

This is a common misconception. If the force sum is zero, the charge moves at constant velocity.

The key point is that you just need a miniscule force above the electric one to start the motion. The key word is "slowly".

 

[Ibix]

Yes and no. You need to apply a different force to start it moving (or change its motion in general). But if the charge is already moving you will have to apply a force qE to keep it moving at constant speed, is all he is saying. The work done by that force goes into the electric field (you are moving a charge and therefore changing the electric field).

Edit: beaten to it by Orodruin.

 

[andrewkirk]

The key is the words 'very slowly'. Strictly speaking they should also replace their 'equal to' by 'infinitesimally greater than'.

The idea is that if F is infinitesimally larger than the electrostatic force for half the time and infinitesimally less than it for the other half, the particle will accelerate very slowly to a very slow maximum velocity in the desired direction, and then decelerate very slowly, to finally come to rest at the destination. Subject to limitations like friction, air resistance and experimental accuracy, we can make this infinitesimal difference as small as we like.

Edit: Haha, beaten to it by Orodruin and Ibix.