Why Is the Photon One-Point Function Zero in QED?

taishizhiqiu
Messages
61
Reaction score
4
In 'an introduction to quantum field theory' by peskin, he writes: To analyze the photon one-point function, note that the external photon must be attached to a QED vertex. Neglecting the external photon propagator, this amplitude is therefore:

upload_2015-10-1_16-44-37.png


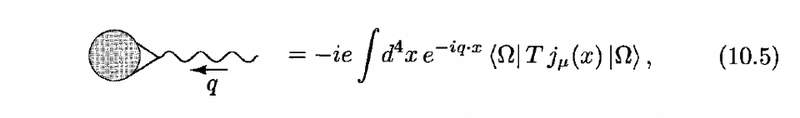
I really cannot justify this equation. Can anyone explain it to me?
 
Intuitively, the expression is essentially the diagram with the two fermion lines and vertex (by definition of j_{\mu}). Note the, "neglecting the external photon propagator." If you include the photon propagator as a factor, the expression gives rise to the same diagram as if the current were to be replaced by the photon field, i.e. the photon one-point correlation function.
 

Thread 'Toponium Discovered'

Toponium is a hadron which is the bound state of a valance top quark and a valance antitop quark. Oversimplified presentations often state that top quarks don't form hadrons, because they decay to bottom quarks extremely rapidly after they are created, leaving no time to form a hadron. And, the vast majority of the time, this is true. But, the lifetime of a top quark is only an average lifetime. Sometimes it decays faster and sometimes it decays slower. In the highly improbable case that...
View full post »

Thread 'Dirac-Delta from Normalization of Continuous Eigenfunctions'

I'm following this paper by Kitaev on SL(2,R) representations and I'm having a problem in the normalization of the continuous eigenfunctions (eqs. (67)-(70)), which satisfy \langle f_s | f_{s'} \rangle = \int_{0}^{1} \frac{2}{(1-u)^2} f_s(u)^* f_{s'}(u) \, du. \tag{67} The singular contribution of the integral arises at the endpoint u=1 of the integral, and in the limit u \to 1, the function f_s(u) takes on the form f_s(u) \approx a_s (1-u)^{1/2 + i s} + a_s^* (1-u)^{1/2 - i s}. \tag{70}...
View full post »

Similar threads

A Confusions on QED renormalization
Replies
1
Views
2K
I QED - running of coupling (beta function)
Replies
5
Views
3K
I QED replacing photon field with current in 3-point function
Replies
1
Views
904
I Are All Photons Truly Virtual?
Replies
6
Views
2K
I QED/Quantum Mechanics: Probability or Spatial Function?
Replies
8
Views
2K
Typical Momentum Invariants of a 3-Point Function
Replies
3
Views
1K
Definition of effective QED coupling.
Replies
2
Views
3K
A How does one find the Feynman diagrams?
Replies
1
Views
2K
A The Quantum State as a Function of The Quantum Field
Replies
13
Views
2K
I How can electrostatic fields be composed of photons?
Replies
30
Views
3K

Hot Threads

Recent Insights

Back
Top