Why is the procedure for finding Va-Vb in the given circuit incorrect?

[sankalpmittal]

Homework Statement

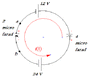
See the image : http://postimg.org/image/hswmylvz1/

In the image, potential of point a is V_a and that of point b is V_b. We have to find out V_a-V_b for the circuit as shown in the image.

Homework Equations

-----

The Attempt at a Solution

Let the potential of negative terminal of the 12 V battery be 0, and its positive terminal's potential be 12 V. Similarly let potential of positive terminal of 24 V battery be 24 V and negative terminal be 0 V. Then potential of a, V_a = 0 and potential of b, V_b=0, and so V_a-V_b=0, but this is wrong. :(

Also, I already got the answer by Kirchoff's loop law, but I wanted to know why above procedure is wrong. Also is the circuit in parallels or in series ?

Please help !

Thanks in advance..

 

[gneill]

For a given circuit there can be only one reference point for potential. You've tried to make the negative pole of both batteries separate zero references. This is equivalent to shorting points a and b, eliminating the capacitor in between.

 

[NascentOxygen]

Also, I already got the answer by Kirchoff's loop law

How many volts have you calculated across each capacitor?

 

[lalo_u]

The right one -> 4 V
The left one -> 8 V

Am i right?

 

[CWatters]

Are there any assumptions to go with the problem? For example regarding the initial state of charge on the capacitors when the circuit is built?

 

[sankalpmittal]

How many volts have you calculated across each capacitor?

Yes, I got -8 V of potential difference across point a and b. That is I got V_a-V_b=-8 V.

For a given circuit there can be only one reference point for potential. You've tried to make the negative pole of both batteries separate zero references. This is equivalent to shorting points a and b, eliminating the capacitor in between.

Means ? The author of the book assumed in one question, the junction of the circuit at zero potential. That will also mean two terminals of the battery at zero potential, if there were two batteries on either side of junction ?

Are there any assumptions to go with the problem? For example regarding the initial state of charge on the capacitors when the circuit is built?

No, the problem was, as I stated.

lalo_u: The right one -> 4 V
The left one -> 8 V

Am i right?

Not sure about right one, but yes, potential difference across capacitor, that is V_b-V_a = 8 V in the left one.

 

[gneill]

Means ? The author of the book assumed in one question, the junction of the circuit at zero potential. That will also mean two terminals of the battery at zero potential, if there were two batteries on either side of junction ?

There can be only one reference point. It's analogous to choosing a reference height for gravitational potential when you're doing mechanics; the zero reference can't be at two different heights, and there can't be two different zeros for the same set of equations describing a system.

You can choose any node in a circuit to be the zero reference. Some choices make analysis simpler or just seem more logical, such as choosing the -ve terminal of the battery. If more than one battery joins at a node (junction) then that node may be a good choice for a reference point.

Note that choosing a zero reference does not effect the potential differences produced by batteries. Rather, it is like having a voltmeter and clipping its negative lead to a single place in the circuit, then using the positive lead to measure potentials at various places in the circuit. All the measurements use the same reference point thanks to the fixed location of the negative lead, and what you can then deduce is the relative differences in potential from place to place in the circuit.

 

[NascentOxygen]

The right one -> 4 V
The left one -> 8 V

Am i right?

4V on the larger capacitor, and 8V on the smaller, since we can assume they have been given identical charge.

 

[anhnha]

Here is my solution. Hope you can check it.
Let's call the left capacitor is C1 and the right one is C2.
Apply KVL for the loop:
Vc1 - 24 + Vc2 + 12 = 0 where Vc1 = Vab
or
Vc1 + Vc2 = 12 V
Because C1 and C2 are in series: Vc1/Vc2 = C2/C1 = 4/2 = 2
Hence, Vc1 = Vab = 8V, Vc2 = 4V.

 

[sankalpmittal]

There can be only one reference point. It's analogous to choosing a reference height for gravitational potential when you're doing mechanics; the zero reference can't be at two different heights, and there can't be two different zeros for the same set of equations describing a system.

You can choose any node in a circuit to be the zero reference. Some choices make analysis simpler or just seem more logical, such as choosing the -ve terminal of the battery. If more than one battery joins at a node (junction) then that node may be a good choice for a reference point.

Note that choosing a zero reference does not effect the potential differences produced by batteries. Rather, it is like having a voltmeter and clipping its negative lead to a single place in the circuit, then using the positive lead to measure potentials at various places in the circuit. All the measurements use the same reference point thanks to the fixed location of the negative lead, and what you can then deduce is the relative differences in potential from place to place in the circuit.

Thank you gneill.

Now can you give me some hints to solve it without using KVL ?

4V on the larger capacitor, and 8V on the smaller, since we can assume they have been given identical charge.

Here is my solution. Hope you can check it.
Let's call the left capacitor is C1 and the right one is C2.
Apply KVL for the loop:
Vc1 - 24 + Vc2 + 12 = 0 where Vc1 = Vab
or
Vc1 + Vc2 = 12 V
Because C1 and C2 are in series: Vc1/Vc2 = C2/C1 = 4/2 = 2
Hence, Vc1 = Vab = 8V, Vc2 = 4V.

anhnha and Nascent, you should get V_ab=V_a-V_b=-8 V.

Where is your "-" sign missing ?

Also, anhnha don't give complete solutions for HW questions in future. Its against the forum rules !

 

[gneill]

Thank you gneill.

Now can you give me some hints to solve it without using KVL ?

I'm not sure why you'd want to do that... it's one of the fundamental circuit laws. Somehow you need to mathematically describe the situation where the circuit is static (steady state), and that involves comparing potential differences, which is the same as writing KVL.

anhnha and Nascent, you should get V_ab=V_a-V_b=-8 V.

Where is your "-" sign missing ?

Also, anhnha don't give complete solutions for HW questions in future. Its against the forum rules !

The net potential from the sources would indicate that the initial current will be counterclockwise (the 24V supply dominates). That will drive the top plate of the 2μF capacitor (where "a" is located) positive, and the bottom plate of the 4μF capacitor positive, too.

 

[sankalpmittal]

I'm not sure why you'd want to do that... it's one of the fundamental circuit laws. Somehow you need to mathematically describe the situation where the circuit is static (steady state), and that involves comparing potential differences, which is the same as writing KVL.

I mean doing it by the concept of finding effective capacitance.

The net potential from the sources would indicate that the initial current will be counterclockwise (the 24V supply dominates). That will drive the top plate of the 2μF capacitor (where "a" is located) positive, and the bottom plate of the 4μF capacitor positive, too.

But the book gives the answer that V_a-V_b=-8 V. There is the minus sign, as per the author of the book, where I have taken this question.

I cannot understand. Sorry.. :(

 

[Saitama]

But the book gives the answer that V_a-V_b=-8 V. There is the minus sign, as per the author of the book, where I have taken this question.

I don't see why a minus sign would come here. Definitely a is at a higher potential than b.

You don't need to find the effective capacitance here. The question asks the potential difference across the 2 micro farad capacitor. You have a "effective" battery of 12 V here. Can you find the potential difference across the two capacitors?

 

[gneill]

I mean doing it by the concept of finding effective capacitance.

Okay, well if you allow the lesson from KVL that tells us the order of potential changes around an isolated loop is irrelevant, then we can shuffle the order of the components (this is equivalent to algebraically reordering the terms in a sum, which we know makes no difference to the total). Group the voltage sources together and capacitors together. Then you have a net voltage source and two capacitors which are clearly in series and you can employ the capacitor potential divider rule.

But the book gives the answer that V_a-V_b=-8 V. There is the minus sign, as per the author of the book, where I have taken this question.

I cannot understand. Sorry.. :(

It may depend upon how the author defines his terminology for V_ab. Is it the potential at a with respect to b, or the potential at b with respect to a? That'll give you a sign difference.

 

[lalo_u]

Ok. Firstly we should assume these capacitors are completely charged. So, we cannot talk about any current in the circuit (the charges don't jump the capacitors).

Secondly, the 24 V power supply is greater than the other one. Then, we must assume that Va > Vb and the "minus sign" of book answer must be wrong.

 

[CWatters]

I think it's been done to death but this is how I'd do it..

Let V₂ be the voltage on C₂ (the 2uF) and V₄ be the voltage on C₄ (the 4uF) and +ve is defined as per gneil's version of the drawing.

Then applying KVL clockwise from "b" says..

V₂ + 12 + V₄ + (-24) = 0

So

V₂ + V₄ = 12

Then if you remember/assume..

1) Q=CV
2) the Capacitors were discharged when the circuit was built
3) the same amount of charge flows through both caps because they are in series

then

C₂V₂ = C₄V₄

Solving these two equations gives

V₂ = 8V
V₄ = 4V

Now V₂ = Va-Vb so

Va-Vb = 8V

However the problem doesn't actually say the caps were discharged so that assumption should be stated in the answer. If you don't make that assumption then all you can say is that

V₂ + V₄ = 12

and you can't give an answer for Va-Vb.

 

[sankalpmittal]

I think it's been done to death but this is how I'd do it..

Let V₂ be the voltage on C₂ (the 2uF) and V₄ be the voltage on C₄ (the 4uF) and +ve is defined as per gneil's version of the drawing.

Then applying KVL clockwise from "b" says..

V₂ + 12 + V₄ + (-24) = 0

So

V₂ + V₄ = 12

Then if you remember/assume..

1) Q=CV
2) the Capacitors were discharged when the circuit was built
3) the same amount of charge flows through both caps because they are in series

then

C₂V₂ = C₄V₄

Solving these two equations gives

V₂ = 8V
V₄ = 4V

Now V₂ = Va-Vb so

Va-Vb = 8V

However the problem doesn't actually say the caps were discharged so that assumption should be stated in the answer. If you don't make that assumption then all you can say is that

V₂ + V₄ = 12

and you can't give an answer for Va-Vb.

Why ? The book asks for V_a-V_b. Also, there is practically no current flow in single direction in capacitors. The negative terminal of the battery supply charge -Q to the circuit and the positive terminal of the battery supply charge +Q charge to the circuit. You seem to be measuring charge flow from negative terminal of battery. From positive terminal, sign will just invert, I think.

Okay, well if you allow the lesson from KVL that tells us the order of potential changes around an isolated loop is irrelevant, then we can shuffle the order of the components (this is equivalent to algebraically reordering the terms in a sum, which we know makes no difference to the total). Group the voltage sources together and capacitors together. Then you have a net voltage source and two capacitors which are clearly in series and you can employ the capacitor potential divider rule.

It may depend upon how the author defines his terminology for V_ab. Is it the potential at a with respect to b, or the potential at b with respect to a? That'll give you a sign difference.

The author asks for, V_a-V_b, which is I think potential of point "a" with respect to "b".

 

[CWatters]

However the problem doesn't actually say the caps were discharged so that assumption should be stated in the answer. If you don't make that assumption then all you can say is that

V2 + V4 = 12

and you can't give an answer for Va-Vb.

Why ? The book asks for Va-Vb. Also, there is practically no current flow in single direction in capacitors. The negative terminal of the battery supply charge -Q to the circuit and the positive terminal of the battery supply charge +Q charge to the circuit. You seem to be measuring charge flow from negative terminal of battery. From positive terminal, sign will just invert, I think.

If a step voltage is applied to a capacitor there is very definitely current flow.

If the caps aren't discharged when the circuit is assembled the batteries aren't the only source of charge.

There are two capacitors so there are other solutions (eg 9V and 3V) which also meet KVL. These that might result if there was charge on the caps when the circuit is built.

 

[sankalpmittal]

If a step voltage is applied to a capacitor there is very definitely current flow.

If the caps aren't discharged when the circuit is assembled the batteries aren't the only source of charge.

There are two capacitors so there are other solutions (eg 9V and 3V) which also meet KVL. These that might result if there was charge on the caps when the circuit is built.

Ok thanks !

I missed the convention that voltage difference along the direction of current is taken as negative while applying KVL. So that is why V_a-V_b=-8 V...

Thanks everyone !