oneplusone
- 127
- 2
Homework Statement
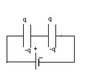
C_1 = 5uF
c_2 = 10uF
C_3 = 2uF
Potential difference between a and b is 60 V.
What is the charged stored on C_3
Homework Equations
C=Q/V
The Attempt at a Solution
See attached.
My question is, why is the charge distribution from A to C the same as the distribution from C to B?
Sorry if the solution is unclear; I find it unclear as well.