Why is there a vertical force on the pin in this static equilibrium setup?

[15ongm]

Q: Why does the pin have a vertical force in this diagram (Static equilibrium)?

The diagram depicts as follows:
A mass (M) sits a a distance (d) away from the end of a board of length L. The board has a mass of m and is held to a wall by a pin and string. The string has a tension (T) and is at angle θ to the board. The pin is frictionless. The entire set-up is in static equilibrium.

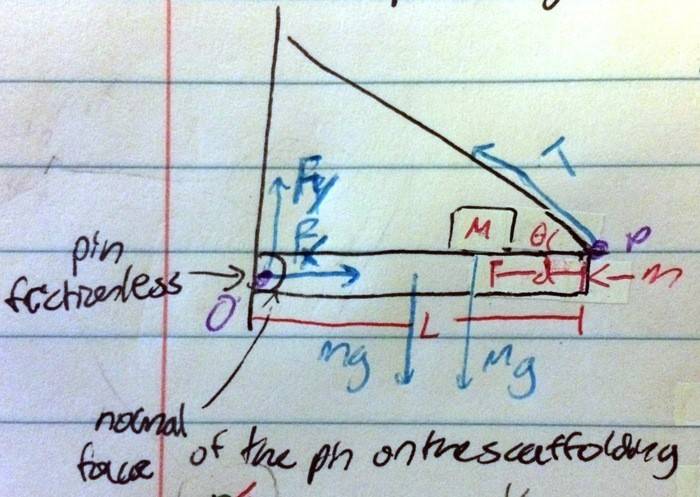
Side note: In the diagram I called the board the scaffolding.

What I don't understand is why the pin has forces (Fy & Fx). I sort of understand why the pin must have a horizontal force (Fx) b/c otherwise there would be no other force to oppose the horizontal competent of tension. What I don't understand is why Fy must exist. To be honest, I don't even understand what Fy really is. Shouldn't the vertical component of the tension be enough to oppose the weight of the block and board? If so, there's no need for another upward vertical force.

I'd be really grateful if anyone could help me on this!

 

[AlephNumbers]

Is the pin stuck to the wall?

 

[haruspex]

What I don't understand is why Fy must exist

Consider moments about some point (that is not on a vertical line through the pin).

 

[NascentOxygen]

Why not experiment? A short length of timber, a piece of rope tied to one end, and a brick. Is the free end of the plank happy to rest against the wall, or do you need to provide vertical supprt to keep it horizontal?

Once you know what happens in reality you can look for the theory that confirms it.

 

[Ananya0107]

What about the torque produced by Tsinθ ? What if we look at the net torque about the centre of mass of the plank ? We may need F_y for rotational equilibrium of the plank.

 

[AdityaDev]

The pin is like a hinge and the name for such forces is Hinge reaction forces.
The vertical component of T might be enough. You have to find it by using Newton's laws.
The hinge reaction plays a very important role when the string is burnt. In such a case, Fx provides centripetal force, while Fy opposes the weight.

 

[Ananya0107]

The pin is like a hinge and the name for such forces is Hinge reaction forces.
The vertical component of T might be enough. You have to find it by using Newton's laws.
The hinge reaction plays a very important role when the string is burnt. In such a case, Fx provides centripetal force, while Fy opposes the weight.

Could we establish static equilibrium without the pin ? I mean just the plank , and the thread ?

 

[AdityaDev]

Could we establish static equilibrium without the pin ? I mean just the plank , and the thread ?

Yes. When you have friction. That is why I said you need to apply Newton's laws. Draw the FBD for the plank.

 

[CWatters]

Shouldn't the vertical component of the tension be enough to oppose the weight of the block and board?

Would you think the same if the mass m was at the pin end of the board?