evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
I am looking at the following:
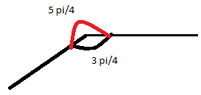
View attachment 5324Why do we take the $\theta$ to lie on $[0, \pi]$ ?
I am looking at the following:
View attachment 5324Why do we take the $\theta$ to lie on $[0, \pi]$ ?