Why isn't the circuit a combinatorial one?

[evinda]

Hello! (Wave)

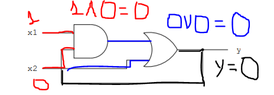
I read the following about parity functions:

View attachment 6679

Since I haven't heard of combinatorial circuits before, I have searched for them.

I have found the following: http://http://www.math.northwestern.edu/~mlerma/courses/cs310-04w/notes/dm-combcirc.pdf
I haven't understood how we deduce that the circuit in figure 8.3 ( page 3 from the link- 120 from the book) is not a combinatorial circuit.
Do we have to find the expression that represents it? If so, how do we do so? (Thinking)

 

[I like Serena]

Hey evinda! (Smile)

It says in the book:

A combinatorial circuit is a circuit whose output is uniquely defined by its inputs. ​

and:

If x1 = 1 and x2 = 0 then y can be 0 or 1.​

So the output is not uniquely defined by its inputs.
And that's why the circuit in figure 8.3 is not a combinatorial circuit. (Thinking)

 

[evinda]

Hey evinda! (Smile)

It says in the book:

A combinatorial circuit is a circuit whose output is uniquely defined by its inputs. ​

and:

If x1 = 1 and x2 = 0 then y can be 0 or 1.​

So the output is not uniquely defined by its inputs.

But, why is it like that? Since at the circuit there aren't said any inputs, we can go anywhere with input either 0 or 1 ?(Thinking)

 

[I like Serena]

But, why is it like that? Since at the circuit there aren't said any inputs, we can go anywhere with input either 0 or 1 ?(Thinking)

I don't understand your question.

The problem is really that there is a (so called feedback) loop in the circuit.
If we verify what happens when x1 = 1, x2 = 0, and y=0, it turns out that all logic gates can work as intended, and that the result is 'true'.
But the same thing applies if we verify what happens with x1 = 1, x2 = 0, and y=1.
Without feedback loops this is not possible, and the output is always unique.

 

[evinda]

I don't understand your question.

The problem is really that there is a (so called feedback) loop in the circuit.
If we verify what happens when x1 = 1, x2 = 0, and y=0, it turns out that all logic gates can work as intended, and that the result is 'true'.

So if we have $x_1=1$ and $x_2=0$ do we have to take the first possible way for $x_2$, then we have the expression $x_1$ AND $x_2$ and get $1 \wedge 0=0$ and then we get $y=0$ ? Or how do we find the value of $y$ ?
Or do we have to take into consideration all the paths for $x_2$ ? I am a bit confused right now. (Worried)

 

[I like Serena]

So if we have $x_1=1$ and $x_2=0$ do we have to take the first possible way for $x_2$, then we have the expression $x_1$ AND $x_2$ and get $1 \wedge 0=0$ and then we get $y=0$ ? Or how do we find the value of $y$ ?
Or do we have to take into consideration all the paths for $x_2$ ? I am a bit confused right now. (Worried)

Let's start at the left with the first AND gate.
Here we are confronted with the feedback loop, while we do not know yet what $y$ is.
Let's keep $y$ unknown for now.
Then we get:
$$(x_1 \land y) = (1 \land y) = y$$
Now we apply the OR gate, yielding:
$$(x_2 \lor y) = (0 \lor y) = y$$
As we can see, whatever $y$ is, that's also what we get back at the end.
So any value of $y$ will do.
That is, there is no unique value of $y$ for the given inputs.

 

[evinda]

Let's start at the left with the first AND gate.
Here we are confronted with the feedback loop, while we do not know yet what $y$ is.
Let's keep $y$ unknown for now.
Then we get:
$$(x_1 \land y) = (1 \land y) = y$$
Now we apply the OR gate, yielding:
$$(x_2 \lor y) = (0 \lor y) = y$$
As we can see, whatever $y$ is, that's also what we get back at the end.
So any value of $y$ will do.
That is, there is no unique value of $y$ for the given inputs.

So does this mean that if we get from $x_i$ to some gate that represents one specific operation $\star$ , will we then apply the operation $x_i \star y$, where $y$ is the unknown result? (Thinking)

 

[I like Serena]

So does this mean that if we get from $x_i$ to some gate that represents one specific operation $\star$ , will we then apply the operation $x_i \star y$, where $y$ is the unknown result? (Thinking)

Yes - but only if there is a feedback loop from the unknown result to that gate.

 

[evinda]

Yes - but only if there is a feedback loop from the unknown result to that gate.

What do you mean with feedback loop?

 

[I like Serena]

What do you mean with feedback loop?

A wire that connects the output of a gate to the input of an earlier gate.
In other words, an output feeds back into an input that was part of getting that output.

 

[evinda]

Let's start at the left with the first AND gate.
Here we are confronted with the feedback loop, while we do not know yet what $y$ is.
Let's keep $y$ unknown for now.
Then we get:
$$(x_1 \land y) = (1 \land y) = y$$
Now we apply the OR gate, yielding:
$$(x_2 \lor y) = (0 \lor y) = y$$
As we can see, whatever $y$ is, that's also what we get back at the end.
So any value of $y$ will do.
That is, there is no unique value of $y$ for the given inputs.

I am confused right now. (Sweating)

I thought that we do the following.

At the beginning we apply the operation $x_1$ AND $x_2$, the result will be equal to , say , $x_3$, then we apply the operation $x_2$ OR $x_3$, and get some result $y$, and then we continue the same procedure with $x_2$ getting the value $y$.

Have I understood it wrong? And as I understood we have an infinite loop, right? (Thinking)

 

[I like Serena]

I am confused right now. (Sweating)

I thought that we do the following.

At the beginning we apply the operation $x_1$ AND $x_2$, the result will be equal to , say , $x_3$, then we apply the operation $x_2$ OR $x_3$, and get some result $y$, and then we continue the same procedure with $x_2$ getting the value $y$.

Have I understood it wrong? And as I understood we have an infinite loop, right? (Thinking)

$x_3$ is supposed to be an input and not a result, isn't it? (Wondering)

And no, we don't necessarily apply AND to $x_1$ and $x_2$. It depends on how the graph is defined.
As it is, doesn't the first AND gate have $x_1$ and the unknown output $y$ as its inputs?

And yes, we have an infinite loop - the feedback loop.

 

[evinda]

$x_3$ is supposed to be an input and not a result, isn't it? (Wondering)

Why? I thought that $x_1$ and $x_2$ are the only inputs... (Thinking)

And no, we don't necessarily apply AND to $x_1$ and $x_2$. It depends on how the graph is defined.
As it is, doesn't the first AND gate have $x_1$ and the unknown output $y$ as its inputs?

But then why is $x_2$ connected to the AND-gate? (Thinking)

 

[I like Serena]

Why? I thought that $x_1$ and $x_2$ are the only inputs... (Thinking)

We could. It's just that in our context $x_i$ is used to denote inputs and $y_i$ for outputs. Perhaps we can use, say, $z_i$ for intermediate results?

But then why is $x_2$ connected to the AND-gate? (Thinking)

Isn't $x_2$ connected to another gate?
Or are we talking about different circuits?
Which circuit are you talking about?

 

[evinda]

We could. It's just that in our context $x_i$ is used to denote inputs and $y_i$ for outputs. Perhaps we can use, say, $z_i$ for intermediate results?

A ok.

Isn't $x_2$ connected to another gate?
Or are we talking about different circuits?
Which circuit are you talking about?

I was talking about this circuit:View attachment 6859

and I meant the red marked path that connects $x_2$ to the AND-gate:View attachment 6860If $x_1=1$ and $x_2=0$, I thought that the following is done:View attachment 6861

Am I wrong? (Thinking)

 

[I like Serena]

I'm afraid that the wire from $x_2$ crosses the other wire and is not connected to it.
It's different for the other intersection of wires on the right side. There is black knot there to indicate that those wires are connected.
So $x_2$ is connected to the second gate and is not connected to the first gate. (Thinking)

 

[evinda]

I'm afraid that the wire from $x_2$ crosses the other wire and is not connected to it.
It's different for the other intersection of wires on the right side. There is black knot there to indicate that those wires are connected.
So $x_2$ is connected to the second gate and is not connected to the first gate. (Thinking)

Ah I think I understand. So after each loop, the result is $y$ and so it is not unique, right? (Thinking)

 

[I like Serena]

Ah I think I understand. So after each loop, the result is $y$ and so it is not unique, right? (Thinking)

$y$ is indeed not unique, but it doesn't change with each loop.
If we assign $y$ the value of $0$, the circuit is consistent.
So $y=0$ is a valid output.
However, the same holds true for $y=1$.
And that's why $y$ is not unique. (Thinking)

 

[evinda]

$y$ is indeed not unique, but it doesn't change with each loop.
If we assign $y$ the value of $0$, the circuit is consistent.
So $y=0$ is a valid output.
However, the same holds true for $y=1$.
And that's why $y$ is not unique. (Thinking)

I understand. And we can repeat the loop as many times as we want, right? (Thinking)

 

[I like Serena]

I understand. And we can repeat the loop as many times as we want, right? (Thinking)

Yep!
To be fair, since the loop doesn't change the first or the second time, it's unlikely to change in a later repetition. (Smirk)

 

[evinda]

Yep!
To be fair, since the loop doesn't change the first or the second time, it's unlikely to change in a later repetition. (Smirk)

Yes, I see... Thanks a lot! (Smirk)