Why so big of a difference in cross section by different sources?

In summary, different laboratories often quote different cross section values for the same reaction, such as the thermal neutron capture reaction 9Be(n, r)10Be. The first four sources (EAF-2010, ENDF/B-VII.1, JEFF-3.1.2, and JENDL-4.0) have similar values, while the last source (TENDL-2011) has a significantly different value. This could be due to TENDL-2011 using a different unit or containing some errors. However, the newer version TENDL-2015 has been found to be in agreement with the other experiments. It is recommended to use the data from the newer versions and be cautious
  • #1
kiwaho
72
1
if you look up the cross section in Janis books, usually for same reaction, different cross sections are quoted by different laboratories.
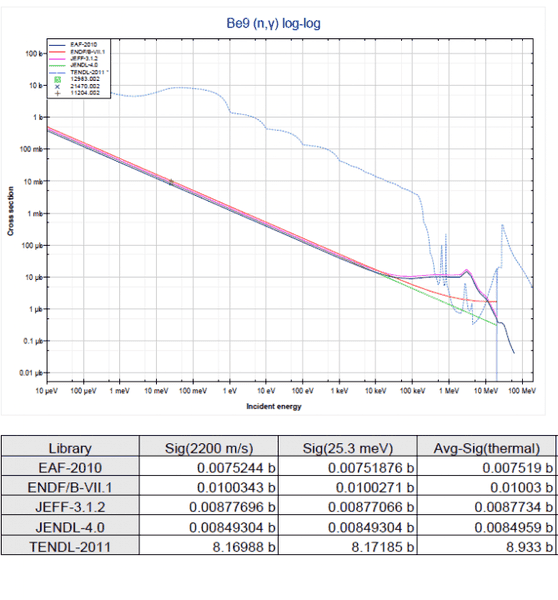
For example, the values of thermal neutron capture reaction 9Be(n, r)10Be:
EAF-2010, 0.0075b
ENDF/B-VII.1, 0.01b
JEFF-3.1.2, 0.0088b
JENDL-4.0, 0.0085b
TENDL-2011, 8.17b
Obviously, the first 4 sources quote very similar values, but the the last source TENDL-2011 quotes a so different value, it is almost 1000 times than previous 4 sources.
How this happen? Which value should be trusted when design?
upload_2016-11-21_14-50-52.png
 

Attachments

  • upload_2016-11-21_14-49-59.png
    upload_2016-11-21_14-49-59.png
    12.5 KB · Views: 519
Physics news on Phys.org
  • #2
My guess TENDL-2011 is using different unit.
 
  • #3
I checked the online version of Janis books, see http://www.oecd-nea.org/janisweb/book/neutrons/Be9/MT102/renderer/263 . There TENDL-2011 has been replaced with TENDL-2015. The new experimental data is in agreement with the other experiments. So, probably the data "TENDL-2011" contained some error.
 
Last edited by a moderator:
  • Like
Likes nrqed
  • #4
there were more than 1 cases where TENDL-2011 gave very weird results compared to others (even some numbers seemed to be buggy)... I am amazed that people actually recorded them...
 

1. Why do different sources show such a large difference in cross section measurements?

The difference in cross section measurements can be attributed to a variety of factors such as the type of equipment used, the accuracy of the measurement technique, and the size and shape of the sample being measured. Additionally, different sources may use different calculation methods or have varying levels of expertise, which can also contribute to the differences in results.

2. How do scientists ensure the accuracy of cross section measurements?

Scientists use a variety of techniques to ensure the accuracy of cross section measurements, such as calibrating equipment, using multiple measurement methods, and cross-checking results with other sources. They also carefully control experimental conditions and minimize sources of error to obtain the most precise measurements possible.

3. Can cross section measurements vary over time?

Yes, cross section measurements can vary over time due to changes in experimental conditions, equipment performance, or the sample itself. Scientists often repeat measurements multiple times to account for any fluctuations and ensure the accuracy and reproducibility of their results.

4. Are there any standard units for cross section measurements?

Yes, the most commonly used unit for cross section measurements in the scientific community is the barn (b), which is equal to 10^-24 cm^2. This unit allows for easier comparison and interpretation of results across different studies and sources.

5. How do scientists use cross section measurements in their research?

Cross section measurements are essential in many fields of science, particularly in materials science, physics, and chemistry. They provide important information about the properties and behavior of materials, as well as allowing scientists to make predictions and develop new technologies based on their findings.

Similar threads

Difference in thermal n cross section for Be-9 and B-10
    • High Energy, Nuclear, Particle Physics
Replies
9
Views
4K
Difference of B-10(n,2a)H-3 cross section in ENDF/B
    • Nuclear Engineering
Replies
9
Views
1K
Cu-65(N,G)Cu-66 Cross Sections
    • High Energy, Nuclear, Particle Physics
Replies
1
Views
3K
Find specific reaction cross section in an ENDF file
    • Nuclear Engineering
Replies
2
Views
5K
Capture Cross Section for a Neutron
    • Engineering and Comp Sci Homework Help
Replies
1
Views
3K
Cross section data, how to fill in the gaps?
    • Nuclear Engineering
Replies
2
Views
2K
Ba-133 Neutron Capture Cross Section - Thermal & Excited States
    • Nuclear Engineering
Replies
8
Views
8K
I Updates on the experiments X17
    • Beyond the Standard Models
2
Replies
39
Views
5K
Film Exposure: The Impact of Light Sources with Different Temperatures
    • Introductory Physics Homework Help
Replies
2
Views
2K
Plasma Creation Method and Ignition of Self-sustained Reaction in Toroidal Reactors
    • Nuclear Engineering
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top