- #1
tgt
- 522
- 2
What is the explanation for the tide on the surface of the Earth opposite the moon?
tgt said:What is the explanation for the tide on the surface of the Earth opposite the moon?
Vanadium 50 said:TGT, Danger's description is the correct one.
Ian said:George,
Imagine that you are swinging on a trapeze.
In this 'you' are the Earth and the 'moon' is the trapeze pivot. If you do a 'loop the loop' as you swing, your hands holding the bar will feel a force toward the pivot - this force represents the higher tide on the side of the Earth facing the moon.
Your shoes however, will try to fly off your feet - this the force represents the tide on the far side of the Earth from the moon.
Like the others said, the key to understanding the tides is to realize that the Earth and moon rotate as one body about a single point.
Georgepowell said:Danger said: "...and then pulls the Earth away from the farthest ocean" which I said I thought was wrong, or at least significantly incomplete.
Danger said:pulls the Earth away from the farthest ocean.
That's a gross oversimplification, but the best that I can contribute.
That's not a good explanation. Think of it this way: The sun and Earth orbit (don't use spin here; that means something different) about their common center of mass, too, and the Sun-Earth center of mass is located *a lot* further from the Earth's center of mass than is the Earth-Moon center of mass.Georgepowell said:The moon does not just simply spin around the earth. The moon and the Earth spin around their common center of mass. i.e. you can treat the moon and the Earth as one object spinning around its own center of mass.
What this leads to, is that the part of the Earth further away from the Earth is like the outer side of a ball being swung round your head, and so the ball elongates in the direction of the point it is spinning from.
D H said:That's not a good explanation. Think of it this way: The sun and Earth orbit (don't use spin here; that means something different) about their common center of mass, too, and the Sun-Earth center of mass is located *a lot* further from the Earth's center of mass than is the Earth-Moon center of mass.
The tidal forces result from the gradient of the gravitational acceleration, and this is to first order an inverse-cube effect. Even though the Sun is much more massive than is the Moon, the Moon has a much greater tidal influence than does the Sun because the Sun is so much further from the Earth than is the Sun.
Yes! An object in freefall directly toward anotherh object (as opposed to being in orbit) feels tidal forces. If you model this as three objects connected via two springs and drop this system from a stationary point above a massive object (and the objects are oriented along that line), both springs will stretch as the three objects are pulled apart.Georgepowell said:Are you saying that if their was no Centrifugal force (I say this with caution, I know it is not a force, just an illusion) then the tide on the other side of the Earth would still be there? If so, what pushes it?
Sure it does. The relevant gravitational acceleration is that relative to the Earth. The relative acceleration toward some third body at the subbody point at its antipodes areGeorgepowell said:Both the sun and the moon exert a gravitational force on the earth, but the difference from one side of the Earth to the other is much greater for the moon's pull than it is for the sun's pull. If I have this right, then I already understood this.
What this explains is why the water is pulled towards the moon less, it is still pulled, just less than on the closer side of the earth. This alone therefore does not explain the tide on the far of the earth; Just because a force is smaller it doesn't make the ocean move further away from the moon.
russ_watters said:Yes! An object in freefall directly toward anotherh object (as opposed to being in orbit) feels tidal forces. If you model this as three objects connected via two springs and drop this system from a stationary point above a massive object (and the objects are oriented along that line), both springs will stretch as the three objects are pulled apart.
People often talk about orbits as situations where centrifugal force equals gravitational force, but this is a little bit of a misleading way of looking at it and tidal forces are an example of why. To be honest, I'm not sure if doing the math on your answer would produce the correct result, but even if it does, it doesn't give a full treatment to the concept of tidal force.
In my example, there is no rotational component, so no centrifugal force.Georgepowell said:I think that we both have the same theory behind the tide, just I might be explaining it differently...
As i have said, the centrifugal force is not a real one, just a tendadncy for objects to stay moving in a straight line. And in your analogy where the three objects on springs are in free-fall, the object on the further side has a tendency to 'stay in the same place' whilst the other parts are falling towards the masive object. So your explanation is really just another way of explaining the centrifugal force.
russ_watters said:If you model this as three objects connected via two springs and drop this system from a stationary point above a massive object (and the objects are oriented along that line), both springs will stretch as the three objects are pulled apart.
No, they are not. Please read post #16 by Vanadium 50, link https://www.physicsforums.com/showthread.php?p=1993649#post1993649".Georgepowell said:OK, let's get this straight; I don't like arguing with someone that I agree with. Firstly, I think your explanation is completely valid, and is virtually the same explanation as mine.
You're right: It agrees with you. And like yours, it's an incorrect explanation. The bulges on the sides of the Earth facing and opposite the Moon do not arise from two different forces, lunar gravity for the near side bulge and inertia (which isn't a force) for the far side bulge. Look at it this way: Lunar gravity extends to infinity. It doesn't stop at the surface of the Earth. Similarly "inertia" (Newton's first law) doesn't stop at the surface of the Earth. It applies to the near side as well as the far side.edit: This agrees with me as well: http://oceanlink.island.net/oinfo/tides/tides.html
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational acceleration experienced by a large body is not constant across its diameter. One side of the body has greater acceleration than its center of mass, and the other side of the body has lesser acceleration.
Inertia is the resistance of an object to a change in its state of motion.
Rather than argue with words, argue with math. Show us, in math, exactly what you are talking about. Doing physics without math is just sophistry.Georgepowell said:I'm going to explain my point via various quotes from Wikipedia
That image most certainly does not include the Earth's gravity. Think about it: If the net force was outward the oceans would long ago have flown off the face of the Earth. You took this image from the Wikipedia article on http://en.wikipedia.org/wiki/Tide#Forces". The caption below the image readsThis image shows that on the right (the moon side of the earth) the gravitational force is greater. And on the left, the inertia is larger, and so that side of the planet does not accelerate as fast towards the moon. And in the centre, they balance out perfectly.
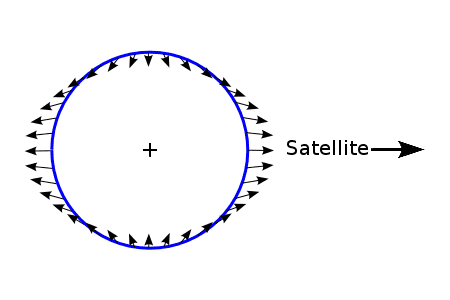
*This also includes the Earth's gravity.*
chis said:Centrifugal or gravity or both?
The mystery of Earth's opposing tide refers to the phenomenon where the tide on one side of the Earth is higher than the other side during certain periods. This is opposite to what is expected from the gravitational pull of the moon and the sun.
The Earth's opposing tide is caused by the Earth's rotation and its shape. As the Earth rotates, the centrifugal force created by its rotation causes the water on the surface to bulge outwards. This creates a high tide on the side of the Earth facing the moon, and a low tide on the opposite side. The Earth's slightly elliptical shape also plays a role in this phenomenon.
The regular tide is caused by the gravitational pull of the moon and the sun. This results in two high tides and two low tides every day. However, the Earth's opposing tide is caused by other factors and occurs only during certain periods, making it different from the regular tide.
The Earth's opposing tide does not cause any significant problems. However, it can affect navigation and water levels in certain areas. It is also an important factor to consider in coastal engineering and construction projects.
No, the Earth's opposing tide has been known for centuries. However, it was not until the 19th century that scientists were able to fully understand and explain this phenomenon. With advancements in technology and research, we continue to learn more about the Earth's opposing tide and its effects.