Why will acceleration be -9.8 if it is moving upward direction?

[nicky670]

Homework Statement

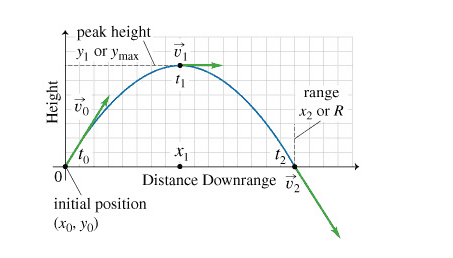
What are the values of the intial velocity vector components v0,x and v0,y (both in m/s) as well as the acceleration vector components a0,x and a0,y (both in m/s2)? Here the subscript 0 means "at time t0."

Relevant Equations

v0x = vocos(angle)
V0y= vosin(angle)

Taking upward direction as positive why will the acceleration be -9.8? Is it due to the curve of the graph?

 

[etotheipi]

The acceleration due to gravity is a downward pointing vector; in the coordinate system shown, with the $\hat{y}$ unit vector pointing upward, it is expressed as $\vec{g} = -g\hat{y}$. That's to say the $y$ component of gravity is $g_y = -g$. When you use SUVAT you are working with the components, so $a_y = g_y = -g$.

 

[nicky670]

So means to say, when working in the y component of the graphs, the acceleration will always be negative due to the gravity and since we take positive as upwards.. And also that gravity is acting downwards, we use sign convention and make it minus?

 

[kuruman]

Taking upward direction as positive why will the acceleration be -9.8? Is it due to the curve of the graph?

No, it's due to the well established fact that objects fall down when you release them from rest and "down" is opposite to "up". So if up is positive, down is negative.

 

[Lnewqban]

So means to say, when working in the y component of the graphs, the acceleration will always be negative due to the gravity and since we take positive as upwards.. And also that gravity is acting downwards, we use sign convention and make it minus?

Another way to see it:
As the projectile goes up, the vertical component of its velocity ($V_y$) gets gradualy reduced until reaching the value of zero.
We could then say that the ascending trajectory is vertically decelerating, since the rate at which the velocity changes is negative ($V_{y2}-V_{y1}$).

The oposite happens during the descending phase of the flight: the direction of the vertical component of the increasing velocity is the same as the acceleration of gravity.

The curve of the graph has nothing to do with that fact: a stone going perfectly vertical up and down will behave exactly like that: up deceleration ($a_y<0$) → instantaneous repose ($a_y=0$) → down acceleration ($a_y>0$).
The curve takes shape due to the combination of simultaneous accelerated vertical movement and horizontal uniform movement ($a_x=0$).

 

[haruspex]

So means to say, when working in the y component of the graphs, the acceleration will always be negative due to the gravity and since we take positive as upwards.. And also that gravity is acting downwards, we use sign convention and make it minus?

I'd express it a little differently.
In principle, you can use whatever sign convention you like for each variable independently, but it's less confusing if you stick with the same two orthogonal directions as positive for all displacements, velocities and accelerations.
In particular, a very standard convention is as for XY graphs, i.e. up and to the right are positive.
If using that then the acceleration due to gravity at Earth's surface is about -9.8m/s², vertically up ( which is the same as saying +9.8m/s² vertically down).

At the risk of confusing you, it has always seemed to me that the symbol g should comply with this convention, i.e. the acceleration due to gravity is g, where g=-9.8m/s². But it seems completely standard to use g for the magnitude, so the acceleration due to gravity is -g, where g=9.8m/s².

 

[Steve4Physics]

"Why will acceleration be -9.8 if it is moving upward direction?"

Hi. Don't forget units!

The direction of acceleration often confuses students. The 'trick' is to remember the direction of acceleration is *always* the same as the direction of the resultant force (F=ma). For projectiles in flight with negligible air resistance, the resultant force is simply the weight which always acts vertically downwards.

By convention we usually take up as positive and down as negative. This makes the weight and vertical acceleration (g) bothe negative.

Think what that actually means. If your throw something upwards, it *slows down* when rising. In fact its vertical speed reduces by 9.8m/s each second (ignoring air resistance). When falling downwards, its vertical speed increases by 9.8m/s each second.

 

[nicky670]

Thank you so much guys!