Why work is PdV and not (P+dP)dV in an isothermal process?

Click For Summary

Discussion Overview

The discussion revolves around the calculation of work done on a gas during an isothermal process, specifically questioning why work is expressed as PdV rather than (P+dP)dV. Participants explore the implications of pressure changes and the mathematical underpinnings of work in thermodynamic systems.

Discussion Character

  • Exploratory
  • Technical explanation
  • Mathematical reasoning

Main Points Raised

  • One participant describes a scenario involving a gas in a cylinder and questions whether the work done should include the additional pressure from a small change in weight on the piston.
  • Another participant states that work is defined as the product of force and distance, leading to the expression W=PdV, where pressure is multiplied by the change in volume.
  • A different participant mentions that the term dP dV is of second order and can be disregarded in calculations.
  • Some participants clarify that the pressure does not need to be constant for the work calculation to hold, using the analogy of a spring to illustrate this point.
  • Concerns are raised about the understanding of differential work and the integration process needed to calculate total work.

Areas of Agreement / Disagreement

Participants express differing views on the necessity of including the term (P+dP) in the work calculation. While some argue that it should be included, others assert that it can be disregarded. The discussion remains unresolved regarding the implications of pressure changes on the work done.

Contextual Notes

Participants exhibit varying levels of familiarity with integral calculus, which may affect their understanding of the mathematical concepts involved in the discussion.

Who May Find This Useful

This discussion may be of interest to students and enthusiasts of thermodynamics, particularly those exploring the mathematical foundations of work in gas systems.

lost captain
Messages
88
Reaction score
7
TL;DR
Why the change in pressure dP is not taken into account when we calculate the work in an isothermal process?
Let's say we have an isothermal compression, isn't the gass compressed due to the initial pressure plus the increase in pressure? If so why work is being calculated as PdV?
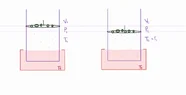
Let's say we have a cylinder of volume V1 with a frictionless movable piston and some gas trapped inside with pressure P1 and temperature T1. On top of the piston lay some small pebbles that add weight and essentially create the pressure P1. Also the system is inside a reservoir of water that keeps its temperature constant at T1.
The system is in equilibrium at V1, P1, T1.

Now let's say i put another very small pebble on top of the piston (0,00001kg)
and after some seconds the system reaches a new equilibrium with
V2<V1 , P2>P1 , T2=T1
What is the work, that has been done to the system?
It s the integral from V1 to V2, in a PV diagram.

What causes the compression, the change in Volume?
Is it the total pressure P1 +dP?
Then shouldn't work be W= (P+dP) × dV and not PdV ?
But then again i don't even understand what dP×dV means. I'm not very advanced in integral calculus maybe that's the reason.


The last part has to do with integral math, I'm sorry if it's not very relevant but i believe it will solve my question to the core :
So I do remember our approach to calculate the area under a graph and that was to "chop" that area in many pieces of dx width and f(x) length and then take the sum of these products, for example one product whould be a specific value f(x1) times the dx of our choice.
Now we have dP times dV, so a change in the function f(x) not a specific value times a change in x?
 

Attachments

  • Φυσική-Μηχανική_250902_233604.webp
    Φυσική-Μηχανική_250902_233604.webp
    7.7 KB · Views: 19
Science news on Phys.org
Work = Fdx=PAdx=PdV
Work=Force times distance
Force= Pressure times area
dV= Area times distance

Corrected
I was sloppy. It is differential work
δW=force times incremental distance
Force= Pressure times area
dV= Area times incremental distance

You can then integrate to get total work.
 
Last edited:
dP dV is infinitesimal of second order. We can disregard it in calculation.
 
Reply
  • Like
Likes   Reactions: lost captain
Frabjous said:
Work = Fdx=PAdx=PdV
Work=Force times distance
Force= Pressure times area
dV= Area times distance
Thank you for replying🙂
The pressure isn't constant though
 
lost captain said:
Thank you for replying🙂
The pressure isn't constant though
It does not have to be. Think about a spring.
 
Last edited:
I was sloppy. It is differential work
δW=force times incremental distance
Force= Pressure times area
dV= Area times incremental distance

You can then integrate to get total work.
 
lost captain said:
I'm not very advanced in integral calculus maybe that's the reason.
Exactly! You should learn it first.
 

Similar threads

Pressure-Volume Work
  • · Replies 5 ·
Replies
5
Views
513
Undergrad Focus Problem for Entropy Change in Irreversible Adiabatic Process
  • · Replies 60 ·
3
Replies
60
Views
10K
Undergrad Graphical difference between adiabatic and isothermal processes.
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad How Do You Calculate Equilibrium Conditions After Mixing Two Different Gases?
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Irreversible adiabatic processes & entropy change (clarification needed)
  • · Replies 22 ·
Replies
22
Views
6K
Undergrad Work in hydrostatic system in cylinder with piston: P_int or P_ext?
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad How Do You Calculate Initial Pressure and Final Volume in Adiabatic Expansion?
  • · Replies 7 ·
Replies
7
Views
2K
High School Energy seems to disappear when gas is compressed?
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Why is P_ext different for reversible and irreversible isothermal expansion?
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Reversible compression of a gas - faulty reasoning?
  • · Replies 2 ·
Replies
2
Views
2K