Will a round-headed rod topple if it slides down a frictionless slope?

[alan123hk]

OK, here's what I can say.

​

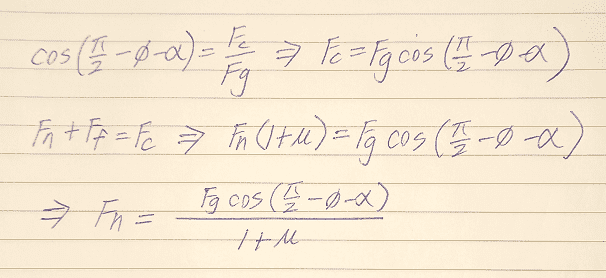
But I still don't know $\theta~$, it's actually the value I'm looking for, so what should we do next?

Edit :
Another interesting thing is $~tan~\theta=\frac{F_n}{F_f}=\frac {1}{u}~~ \Rightarrow~~\theta={tan}^{-1}\left( \frac{1}{u}\right)$
If we substitute it into above equation, we can get $F_n$
But isn't $\theta$ the answer I am looking for? Why can it be found directly by $u$?
If so, why do I need to do so many other complicated derivations? I feel really lost.
Maybe it's as simple as that if friction doesn't vary with speed and no other complex stuff is involved.

 

[jbriggs444]

Another interesting thing is $\theta={tan}^{-1}\left( \frac{1}{u}\right)$

But isn't $\theta$ the answer I am looking for? Why can it be found directly by $u$?
If so, why do I need to do so many other complicated derivations? I feel really lost.

If you look up at #108, you may notice:

arc cotangent of the coefficient of friction

The free body diagram, writing down the force balance equations and torque balance equations and solving the resulting et of simultaneous equations is the brute force crank-and-grind method to solving problems of this sort. It essentially always works.

But more efficient shortcuts can exist. For the frictionless case, a number of participants here were able to immediately intuit that "perpendicular to the slope" was the answer. That answer also falls out of the arctangent of one over the coefficient of friction or [equivalently] the arc cotangent of the coefficient of friction

 

[alan123hk]

The free body diagram and writing down the force balance equations and torque balance equations and solving the set of simultaneous equations is the brute force crank-and-grind method to solving problems of this sort. It essentially always works. But more efficient shortcuts can exist. For the frictionless case, a number of participants here were able to immediately intuit that "perpendicular to the slope" was the answer. That answer also falls out of the arctangent of one over the coefficient of friction or [equivalently] the arc cotangent of the coefficient of friction

Okay, I'm basically satisfied with my understanding of the problem now. As for the advanced calculation method, I need time to study it. Thank you very much for your help.

 

[alan123hk]

I finally got it, it turns out that the explanation is very simple, no complicated math.

In the absence of friction, no matter what the shape of the object, as long as the slope normal vector at the point where the slope intersects the object passes through the object's center of mass, the normal force $F_n$ will not produce a twisting force and the object will remain unrotated. Conversely, if this normal vector does not pass through the object's center of mass, then a twisting force is created to rotate the object.

In addition, regardless of the rotating state or the non-rotating state, the acceleration of the object's center of mass sliding down the slope remains the same and should be equal to $\frac{F_g~sin(\alpha)}{m}$. But if the object is rotating, the torque applied to it seems to vary with its angle and profile, so its angular velocity change should be a fairly complex process.