sirsmokealot
- 4
- 0
hi, i got a question
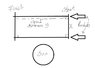
Lets say we got 2 rockets X km appart, traveling parallel to each other in a straight line at the same constant speed. Now let's put a massive object like the Sun on one of sides on the plane the two spaceships make. Which one will get to the finish line first? Would the gravity of the Sun make one of the rockets get there first because gravity "distorts" time or will they pass the finish line simultaneously?
Sorry for my explanation, hard to explain myself in english when its not my native language. But this picture should clarify.
Lets say we got 2 rockets X km appart, traveling parallel to each other in a straight line at the same constant speed. Now let's put a massive object like the Sun on one of sides on the plane the two spaceships make. Which one will get to the finish line first? Would the gravity of the Sun make one of the rockets get there first because gravity "distorts" time or will they pass the finish line simultaneously?
Sorry for my explanation, hard to explain myself in english when its not my native language. But this picture should clarify.