Will the ball rotate on a frictionless slope?

[aerograce]

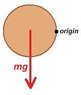
There is a ball placed on a frictionless slope. As we all know that, since there is no friction, the ball will not rotate. But after drawing a free-body-diagram and decomposing the gravity, we find that the net force mgsinθ has a torque relative to the contacting point with the value of mgsinθR. Then it means that, relative to the contacting point, the ball will rotate. It seems that I am in a dilemma now. Can anyone help me explain this？

 

[TSny]

Welcome to PF, aerograce.

It might help to think through a somewhat simpler problem. Imagine dropping a circular disk from rest so that it falls vertically downward with no rotation. The force of gravity is the only force acting on the disk. At some arbitrary time during the fall, suppose you choose a point on the rim of the disk as origin for calculating torque, as shown in the figure. Is there a net torque about this point? If so, why doesn't the disk rotate?

 

[Simon Bridge]

The ball does not roll, it slides.
The observation that there would be a torque about the contact point is correct - but, without the friction, the contact point cannot act as a pivot for the torque.

To see this, draw the free-body diagram.
[edit]Ah TSny beat me to it...

 

[haruspex]

It will acquire angular momentum relative to the contact point: linear velocity x orthogonal displacement. But that does not mean it will rotate. To rotate it must acquire angular velocity about its mass centre.