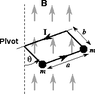
To begin solving this problem, we can use the fact that the loop is in equilibrium to set up equations for the sum of forces and torque. Since the loop is not moving, the sum of forces in the vertical direction must equal zero, and the sum of forces in the horizontal direction must also equal zero. Additionally, the torque about any point must also equal zero.
First, let's consider the sum of forces in the vertical direction. The only forces acting in this direction are the weight of the masses and the magnetic force. The weight of the masses can be calculated using the formula F = mg, where m is the mass and g is the acceleration due to gravity. Since there are two masses, the total weight is 2mg. The magnetic force can be calculated using the formula F = ILB, where I is the current, L is the length of the wire, and B is the magnetic field. In this case, L is equal to the height of the loop b. So the equation for the sum of forces in the vertical direction is:
2mg - ILB = 0
Next, let's consider the sum of forces in the horizontal direction. The only force acting in this direction is the tension in the wire. Since the wire is massless, the tension is the same throughout the wire. So the equation for the sum of forces in the horizontal direction is:
T = 0
Finally, let's consider the torque about the point where the wire is suspended. The torque is equal to the force multiplied by the distance from the point of rotation. In this case, the force is the weight of the masses, and the distance is the width of the loop a. So the equation for the torque is:
2mga = 0
Now we have a system of three equations with three unknowns (T, I, and theta). We can solve for these unknowns using algebraic manipulation. Once we have the values for T and I, we can use them to find the value of theta.
After solving the equations, we get the following values:
T = 0
I = 0.20 Amps
theta = 0°
This means that the loop is in equilibrium when it is hanging vertically, with no angle. This makes sense since the sum of forces and torque are equal to zero, and the loop is not moving.