Work Done by moving point charge

In summary, the conversation is about determining the amount of work required to bring a charge of +5q from infinity to a specific point near two fixed charges +4q and -2q. The distance between the charges is 1.40 cm and the charge is q = 1.6 × 10–19 C. The speaker suggests using the potential at the point, which they calculated to be 0 Volts, and the equation W = qt(Vp-Vinfinity) = 0J. However, the image provided by the other person is not visible, making it difficult to solve the problem without knowing the relative positions of all the charges. The other person then asks for a description of the particle positions using a coordinate system
  • #1
DANIELLYMA
16
0
Hi I think I figured it but I'm not sure.

Here's the problem:

How Much Work In Fig. 25-34, how much work is required to bring the charge of +5q in from infinity along the dashed line and place it as shown near the two fixed charges +4q and –2q? Take distance d = 1.40 cm and charge q = 1.6 × 10–19 C.

2md2p87.gif
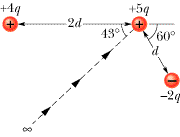I summed up the Vpotential at the point which I got 0 Volts

Then I used W = qt(Vp-Vinfinity) = 0J. It just seems too simple to be correct.
 
Last edited:
Physics news on Phys.org
  • #2
You image does not open. Can you describe it?
 
  • #3
This can't be solved without knowing the relative spacings of all the charges. The net repulsion/attraction will determine how much potential energy is stored by the work. Can you describe the particle positions using a coordinate system?
 
  • #4
Edit: I reuploaded the picture, thanks for your replies
 

FAQ: Work Done by moving point charge

1. What is work done by a moving point charge?

The work done by a moving point charge is the product of the charge's magnitude and the component of its velocity in the direction of the force acting on the charge. It is a measure of the energy transferred to or from the charge as it moves in an electric or magnetic field.

2. How is the work done by a moving point charge calculated?

The work done by a moving point charge can be calculated using the equation W = qVcosθ, where q is the charge, V is the velocity of the charge, and θ is the angle between the direction of the force and the direction of the charge's motion.

3. What is the relationship between work done by a moving point charge and its potential energy?

The work done by a moving point charge is equal to the change in the charge's potential energy. This means that if the charge's potential energy decreases, the work done on the charge is positive, and if the potential energy increases, the work done is negative.

4. How does the work done by a moving point charge affect its kinetic energy?

The work done by a moving point charge can either increase or decrease the charge's kinetic energy, depending on the direction of the force. If the force is in the same direction as the charge's motion, the work done will increase the kinetic energy. If the force is in the opposite direction, the work done will decrease the kinetic energy.

5. What are some real-world applications of the concept of work done by a moving point charge?

The concept of work done by a moving point charge has many real-world applications, including the operation of electric motors and generators, the production of electricity in power plants, and the movement of charged particles in particle accelerators. It is also an important concept in understanding the behavior of lightning and other atmospheric phenomena.

Similar threads

Some confusion about work done to separate charges
Replies
11
Views
2K
Find the amount of work to move a particle from point A to B
Replies
4
Views
1K
Why is the work done in moving a charge around a circular path zero?
Replies
1
Views
893
Work done in assembling a system of charges
Replies
1
Views
3K
Work done by moving a point charge
Replies
7
Views
3K
Calculating the work done using a line integral
Replies
6
Views
3K
Uniform distribution of charge and work needed
Replies
12
Views
3K
Work done by moving a point-charge
Replies
8
Views
2K
Work done moving charge near a line of charge
Replies
2
Views
1K
Work to bring a charge to the center of two quarter circles
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top