Titan97
Gold Member
- 450
- 18
When a particle is attached to a rope and rotated, then tension acts perpendicular to displacement and work done is zero. But I am thinking about this case (top view):
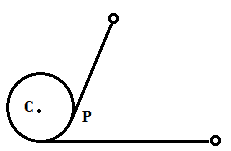
Here, the rope is attached to a vertical cylinder and the particle is given a velocity perpendicular to the rope. The length of rope that's in motion decreases and the particle comes closer and closer to the cylinder. Hence, can I say that the particle moves towards the point P which is along the direction of T. Hence Tension does work. Am I correct?
Another problem is gravity. The particle can go downwards (into the plane of webpage) due to gravity. Let me assume that there is no acceleration due to gravity.
(I have not taken this from any book. I used MS paint to draw this)
Here, the rope is attached to a vertical cylinder and the particle is given a velocity perpendicular to the rope. The length of rope that's in motion decreases and the particle comes closer and closer to the cylinder. Hence, can I say that the particle moves towards the point P which is along the direction of T. Hence Tension does work. Am I correct?
Another problem is gravity. The particle can go downwards (into the plane of webpage) due to gravity. Let me assume that there is no acceleration due to gravity.
(I have not taken this from any book. I used MS paint to draw this)
 .
.