- #1
Ocata
- 198
- 5
Does this derivation:

...imply:
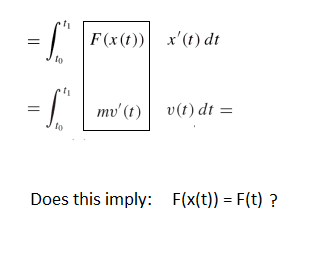 My best guess is that x(t) ≠ t
My best guess is that x(t) ≠ t
So I would also guess that F(x(t)) ≠ F(t)
But then how can this derivation be explained?
How can F(x(t)) = m(a(t))? What does that actually mean?
How come it's not: F(x(t)) = m(a(x(t))) ? Why/How does the x just cancel out? Thank you
...imply:
So I would also guess that F(x(t)) ≠ F(t)
But then how can this derivation be explained?
How can F(x(t)) = m(a(t))? What does that actually mean?
How come it's not: F(x(t)) = m(a(x(t))) ? Why/How does the x just cancel out? Thank you