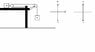matineesuxxx
- 77
- 6
Homework Statement
(see attatchment)
We know masses M and m, and I am trying to describe the downward speed of m in terms of the hight from the ground. There is no friction
Homework Equations
\sum \text{F} = ma
W_{\text{total}} = \Delta K = \int \text{F} \cdot d\text{s}
The Attempt at a Solution
I first need to note that the distance moved by M is half of that moved by m and thus the acceleration of M is half that of m, or a_M = a_m/2.
I first solved the problem using only Newtons laws, so from the FBD I solved for the acceleration of m:
$$a_m = v\frac{dv}{dh} = \frac{mg}{M/4 + m} \implies v = \sqrt{\frac{2mgh}{M/4 + m}}$$
Now if I use the Work-Energy principle, I get that W_{\text{total}} = W_{\text{tension}_x} + W_{\text{tension}_y} + W_g.
This is where I think I am not understanding something:
Work done by tension on M is equal to the work done by tension on m even though force of tension on M is twice that of the force of tension on m because it travels half the distance, and since tension acting on m is acting opposite the direction of motion, it is negative, so W_{\text{tension}_x} = -W_{\text{tension}_y}, so
$$W_{\text{total}} = W_g = mgh = \frac{1}{2}(m + M)v^2 = \Delta K $$
so
v = \sqrt{\frac{2mgh}{m+M}}
I am not sure what I am missing that gives me m+M instead of m + M/4 in the denominator. I would appreciate some help!
Thanks
[EDIT] The answer in the back of the book is the same as the answer I got using Newtons laws
Attachments
Last edited: