Work is not done by static friction when accelerating a car

[kuruman]

A recent thread posed the question whether work is done by static friction in the case of an accelerating car. Before I had a chance to reply, the thread was closed on the grounds that the subject was "beaten to death". Undaunted, I am determined to deliver the coup de grâce here with a simple derivation.
We assume rolling without slipping. Let
$I_{cm}=qmR^2~~~(0 \leq q\leq 1)$ = the moment of inertia of the wheel, radius $R$ and mass $m$, about its CM.
$F$ = the force acting on the wheel at the CM; it is the torque on the wheel divided by the radius $R$.
$f$= the force of static friction on the wheel.

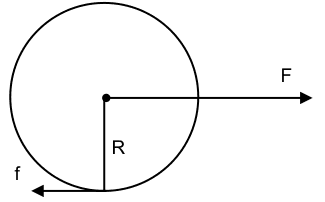
From the FBD shown above, we get
$F-f=ma_{cm}$
$fR=I_{cm}\alpha=qmR^2(a_{cm}/R)$
These equations give
$a_{cm}=\dfrac{F}{(q+1)m}~\rightarrow~\alpha=\dfrac{F}{(q+1)mR};~~~~f=\dfrac{qF}{q+1}$
We invoke the SUVAT equation sans time in the linear and rotational forms to find the changes in translational and rotational kinetic energy, after the CM of the wheel has advanced by $\Delta s_{cm}$.
$$\Delta K_{trans}=\frac{1}{2}m(2a_{cm}\Delta s_{cm})=\frac{1}{2}m\left[2\frac{F}{(q+1)m}\Delta s_{cm}\right]=\frac{F\Delta s_{cm}}{(q+1)}$$
$$\Delta K_{rot}=\frac{1}{2}I_{cm}(2\alpha\Delta \theta)=\frac{1}{2}qmR^2\left[2\frac{F}{(q+1)mR}\frac{\Delta s_{cm}}{R}\right]=\frac{qF\Delta s_{cm}}{(q+1)}=f\Delta s_{cm}$$Interpretation
The input work crossing the system boundary is $F\Delta s_{cm}$ and is equal to $\Delta K=\Delta K_{trans}+\Delta K_{rot}$ in agreement with the work-energy theorem. Static friction does no work on the system but partitions the input work between two internal degrees of freedom, translational and rotational, according to the size of parameter $q$. Specifically, $f\Delta s_{cm}$ is the amount of input work diverted into change in rotational energy. When $q=0$ (point mass) all the input work goes into translational internal energy; when $q=1$ (a ring with all the mass at $R$) we have equipartition of energy. R.I.P.

Note: It often helps to view energy transformations in terms of the first law of thermodynamics. This idea is presented among others in a trilogy of insight contributions currently under preparation.

 

[rcgldr]

I don't understand the FBD. I assume these are the forces exerted onto the wheel. The static friction force at the contact point should be greater than the opposing force at the axle, corresponding to forwards acceleration of the wheel. I assume the opposing force at the axle is the reaction (to acceleration) force from the rest of the vehicle.

I'm not sure how torque should be shown in a FBD.

 

[kuruman]

I don't understand the FBD. I assume these are the forces exerted onto the wheel. The static friction force at the contact point should be greater than the opposing force at the axle, corresponding to forwards acceleration of the wheel. I assume the opposing force at the axle is the reaction (to acceleration) force from the rest of the vehicle.

I'm not sure how torque should be shown in a FBD.

$F$ is the net external horizontal force acting at the CM of the wheel. Yes, torque cannot be easily shown in a FBD, that is why it has been replaced by a force divided by the radius of the wheel. Its composition is irrelevant. The net horizontal force must be in the forward direction and greater than static friction because $a_{cm}$ is directed forward. The force of static friction $f$ is whatever is necessary to provide the observed forward acceleration.

The point of this exercise is to show that if a wheel is accelerated by a horizontal force $F$, then (a) the work input is $F\Delta s_{cm}$ and (b) $f\Delta s_{cm}$ is not the work done by friction but the amount of input work that is converted to rotational energy. The balance of the input work is converted to translational energy.

 

[Dale]

With that, I think we will close this topic. Again.

 

[davenn]

With that, I think we will close this topic. Again.

but you didn't

 

[rcgldr]

Assuming that "forward" in the FBD is to the right, then it appears that the FBD is a image of a wheel being pulled by a string at the axle with force $F$, and that static friction force is an opposing force $f$, causing the wheel to roll as it moves to the right.

For the accelerating car case, a FBD should have a static friction force at the bottom of the wheel, pointed to the right, which is the direction of acceleration, and a reactive (the reaction of the rest of the car to acceleration) force acting on the axle of the wheel, pointed to the left. The static friction force would be greater than the reactive force, corresponding to a net forwards (right) force, resulting in a forwards (right) acceleration of wheel (and car).

 

[vanhees71]

Well, fbd's are not the simplest way to understand things. I'd use the Hamilton formalism. It's clear that forces due to constraints don't do work, which is easily shown using the Lagrange-multiplier concept to impose the constraints, which leads to a simple derivation of the forces due to the constraints and the fact that they don't "do work".

It's of course different as soon as you take into account dissipation. There mechanical work is transferred to heat.

 

[Dale]

but you didn't

Oops! Done