- #1
mikejm
- 40
- 2
I am working on a synthesizer project and have reached a point that I am stumped on.
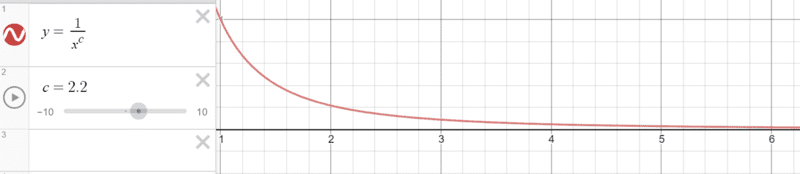
I am in this part trying to work from a basic curve of y=1/x^c (where x≥1):
As I understand, area under the curve between x=1 and x=100,000,000 (ie. more than I need for a rough approximation) would be:
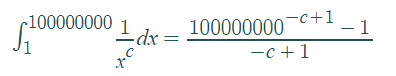
(Symbolab Integral calculator link)
So essentially,
AUC = (100,000,000^(-c+1) - 1)/(-c+1)
Can this equation be re-arranged to roughly approximate for "c="?
I would like to be able to give an "AUC" level between an arbitrary range, and from each AUC level given, calculate approximately "c". This "c" will then be put back into the original y=1/x^c equation. The shape of the y=1/x^c curve will then dictate a part of the synth's sound.
The point is to be able to adjust the y=1/x^c curve with a knob based on "AUC" rather than directly based on "c", as "AUC" makes more sense in this case.
Is this possible to do even approximately in this way?
Thanks a lot,
Mike
I am in this part trying to work from a basic curve of y=1/x^c (where x≥1):
As I understand, area under the curve between x=1 and x=100,000,000 (ie. more than I need for a rough approximation) would be:
(Symbolab Integral calculator link)
So essentially,
AUC = (100,000,000^(-c+1) - 1)/(-c+1)
Can this equation be re-arranged to roughly approximate for "c="?
I would like to be able to give an "AUC" level between an arbitrary range, and from each AUC level given, calculate approximately "c". This "c" will then be put back into the original y=1/x^c equation. The shape of the y=1/x^c curve will then dictate a part of the synth's sound.
The point is to be able to adjust the y=1/x^c curve with a knob based on "AUC" rather than directly based on "c", as "AUC" makes more sense in this case.
Is this possible to do even approximately in this way?
Thanks a lot,
Mike
Attachments
Last edited:



