How can the Newton-Raphson method be used to solve a curved triangle equation?

[m1ke_]

I'm having a hard time figuring out what to do here and it feels as though it involves converting the function into polar coordinates but I'm not a hundred percent sure.

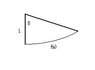
Essentially, I have a triangle in which two sides are straight and one side is a curved function. Knowing only the length of one side, the angle between them, and the function, I need to either be able to find the other straight side or x. I do not need help with solving it but more so just guidance on how I would go about solving it. I've included a mspaint attempt at drawing it.

Thanks in advance

 

[Redbelly98]

What is your application? Or is this a homework or self-study problem?

 

[m1ke_]

The application is towards image processing. I am a coop student and am deriving equations for a project so I cannot go into very much detail.
I've tried using polar coordinate system but my equation blows up when I approach 90 degrees, arc length seems like a reasonable approach but I am not fully certain on what to do.

 

[Redbelly98]

Okay, we are careful around here about helping people with homework. So it's good to know this is not a homework problem

.

I guess you've tried some obvious ways to do this, but let me just suggest the first thing that comes to my mind. There may be reasons why it won't work; if so I'll leave it to you to provide more info.

May I presume line L is in a known orientation (perhaps vertical)? That means the slop of the other straight side -- let's call it M -- is known.

From the slope of M and the coordinates of the common vertex of L and M, you can write an equation for M in y=mx+b form. Then you need to solve for the intersection of the line with f(x); there are standard techniques for doing this numerically.

Once you know the common vertex of L and M, as well as the intersection of M with f(x), you can get the length of M using the Distance Formula from geometry.

The application is towards image processing. I am a coop student and am deriving equations for a project so I cannot go into very much detail.
I've tried using polar coordinate system but my equation blows up when I approach 90 degrees, arc length seems like a reasonable approach but I am not fully certain on what to do.

Hmmm, when θ is 90°, the line is simply y=whatever (the y-coordinate of the vertex common to L and M. Not sure why that would be a problem.

 

[m1ke_]

Okay, we are careful around here about helping people with homework. So it's good to know this is not a homework problem
.

I guess you've tried some obvious ways to do this, but let me just suggest the first thing that comes to my mind. There may be reasons why it won't work; if so I'll leave it to you to provide more info.

May I presume line L is in a known orientation (perhaps vertical)? That means the slop of the other straight side -- let's call it M -- is known.

From the slope of M and the coordinates of the common vertex of L and M, you can write an equation for M in y=mx+b form. Then you need to solve for the intersection of the line with f(x); there are standard techniques for doing this numerically.

Once you know the common vertex of L and M, as well as the intersection of M with f(x), you can get the length of M using the Distance Formula from geometry.


Hmmm, when θ is 90°, the line is simply y=whatever (the y-coordinate of the vertex common to L and M. Not sure why that would be a problem.

Its understandable for your skepticism, and so thank you for your time. I guess I could be a little less vague. Your correct the orientation is vertical and also the function is an exponential function, we can say exp(x).

I just finished trying your method, it works to a point. When I equate the linear function with the known exponential function, it requires a 'Lambert W" (also known as "Product Log") function. I will look into these functions, but at the same time, are there any other suggestions you could make?

 

[Redbelly98]

Okay, glad I was pretty much on target with things.

You have to solve an equation that looks something like

Ae^kx = mx + b​

or

g(x) = Ae^kx - (mx + b) = 0​

You can use the Newton-Raphson method to do this numerically; it is described here:

http://en.wikipedia.org/wiki/Newton's_method​

You'll need an initial trial value for x. I suggest using a very large value for x to guarantee convergence to the desired solution. If theta is close to 90 degrees, or greater, than a small trial value of x will give problems. If you have some idea of the largest x could possibly be in practice, that would be a good initial value.

Hope that helps.

 

[m1ke_]

Okay, glad I was pretty much on target with things.

You have to solve an equation that looks something like

Ae^kx = mx + b​

or

g(x) = Ae^kx - (mx + b) = 0​

You can use the Newton-Raphson method to do this numerically; it is described here:

http://en.wikipedia.org/wiki/Newton's_method​

You'll need an initial trial value for x. I suggest using a very large value for x to guarantee convergence to the desired solution. If theta is close to 90 degrees, or greater, than a small trial value of x will give problems. If you have some idea of the largest x could possibly be in practice, that would be a good initial value.

Hope that helps.

Yes, it does help. I remember that sort of process from class when told to approximate the value of $$\sqrt{}2$$ without a calculator. Never even crossed my mind to use it outside of that. Thank you very much for your help