uperkurk
- 167
- 0
So I have these two straight line equations:
y = -x + 1, y = 2x + 1 So now I have a single point of intersection of (1y,0x)
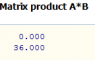
But the next part of the question is what confuses me but I've included a picture as it's just easier... would someone please be able to take the time to explain each step in the question?
I can do parts B and C but A is confusing me...
y = -x + 1, y = 2x + 1 So now I have a single point of intersection of (1y,0x)
But the next part of the question is what confuses me but I've included a picture as it's just easier... would someone please be able to take the time to explain each step in the question?
I can do parts B and C but A is confusing me...