- #1
Mr Davis 97
- 1,462
- 44
Homework Statement
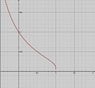
##\displaystyle \int_0^1 \frac{1}{\lfloor 1- \log_2 (1-x)\rfloor}##
Homework Equations
The Attempt at a Solution
How in general do I approach integrals with floor functions? I'm thinking maybe I can figure out what the function in the integrand looks like on paper and calculate the area manually, but that seems very tedious...