- #1
12Element
- 9
- 1
- Homework Statement
- Integration by substitution technique for quadratic equation in square root.
- Relevant Equations
- intSqrt(q+px+X^2)dx
Hi,
With respect to the techniques mentioned in point 2 and 3:

Can someone explain or even better, post a link for an explanation or a videos showing the use of these two techniques.
Below excerpt shows problems 4 and 5 referenced in the above 2 points:
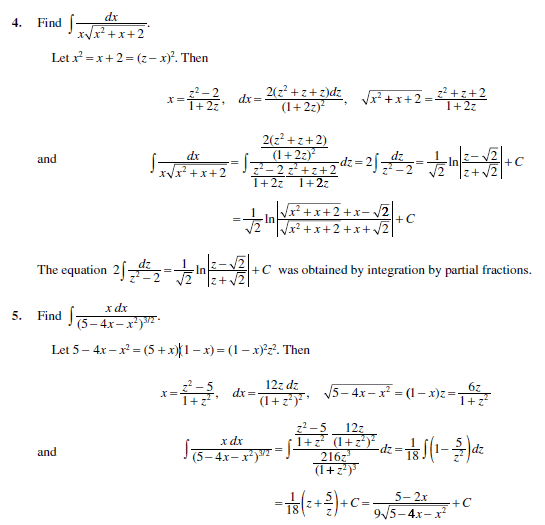
With respect to the techniques mentioned in point 2 and 3:
Can someone explain or even better, post a link for an explanation or a videos showing the use of these two techniques.
Below excerpt shows problems 4 and 5 referenced in the above 2 points: