minnicaj
- 2
- 0
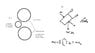
I'm trying to design a automatic tennis ball pitching machine for my senior design project. I will be using two spinning wheels as the launching mechanism. So far I've found the initial velocity after the ball leaves the two spinning wheels (v = 33.398 ft/s). This velocity was found by using the equation R=v^2 sin2θ. Right now I'm having trouble figuring out the forces while the ball is in contact with the two rotating wheels.
One rotating wheel:
Diameter - 6 inches
weight - 1.5 lbs
circumference = 1.57 ft
Tennis ball:
weight: 0.026 lbs
diameter: 2.7 inches
So far the equation I've been using to try and solve this is:
mv_1+∑▒〖∫_(t_1)^(t_2)▒Fdt=mv_2 〗
My professor told me I need to find the forces involved while the ball is in contact with the two wheels so I can calculate the torque needed and select a motor.
Also I've found the rpm's that the wheels would need to be spinning for the ball to have the exit velocity needed to be 1299.36 rpm.
I've also added a picture trying to illustrate my problem and what I've done so far.
Thanks in advance for any help!
One rotating wheel:
Diameter - 6 inches
weight - 1.5 lbs
circumference = 1.57 ft
Tennis ball:
weight: 0.026 lbs
diameter: 2.7 inches
So far the equation I've been using to try and solve this is:
mv_1+∑▒〖∫_(t_1)^(t_2)▒Fdt=mv_2 〗
My professor told me I need to find the forces involved while the ball is in contact with the two wheels so I can calculate the torque needed and select a motor.
Also I've found the rpm's that the wheels would need to be spinning for the ball to have the exit velocity needed to be 1299.36 rpm.
I've also added a picture trying to illustrate my problem and what I've done so far.
Thanks in advance for any help!