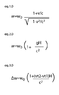Discussion Overview
The discussion centers on the equivalence of time dilation experienced by clocks in different gravitational and accelerating frames. Participants explore the implications of the principle of equivalence, particularly how time dilation manifests in these contexts, and whether it remains constant or varies over time.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- Some participants assert that two clocks in a gravitational field separated by altitude exhibit constant time dilation, while those in an accelerating frame show non-constant time dilation.
- Others argue that the time dilation in an accelerating frame can be constant if the distance between the clocks does not change.
- One participant claims that the frequency of light signals increases as measured by a clock at the back of an accelerating frame, suggesting that the time dilation is non-constant.
- Another participant challenges this view, stating that in a uniformly accelerating frame, the clock rates are constant as measured by an observer at rest in that frame.
- There is a discussion about the equivalence principle, with references to its weak and strong forms, and how they relate to the observations made in gravitational versus accelerating frames.
- Some participants discuss the implications of Doppler shifts in light signals as they travel between clocks in an accelerating frame, questioning whether these shifts affect the measurements of time dilation.
- There are claims that the principle of equivalence does not imply that all gravitational fields are equivalent to all accelerating frames, highlighting nuances in the interpretation of the principle.
Areas of Agreement / Disagreement
The discussion remains unresolved, with multiple competing views on whether time dilation in accelerating frames is constant or non-constant, and how the principle of equivalence applies in different contexts.
Contextual Notes
Participants reference specific conditions such as the distance between clocks and the nature of acceleration, indicating that assumptions about these factors significantly influence their arguments. There is also mention of the need for careful consideration of the definitions and contexts of the equivalence principle.