scholio
- 159
- 0
Homework Statement
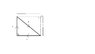
three infinitely long straight wires are arranged in a plane as shown at the left. what is the magnetic field vector at point A(see attach.)? all wires carry current I
Homework Equations
F = IL X B where x indicates cross product, I is current, L is length, B is magnetic field
magnetic field, biot-savart law, B = mu_0/4pi[integral(IdL/r^2)] where mu_0 is constant = 4pi*10^-7, dL is change in length, r is radius/distance, I is current
The Attempt at a Solution
not too sure about how to start, this is what i am thinking of:
first, determine the net magnetic field at the center of the triangle formed by the three wires, and then use the distance from the center of that triangle to point a, as value r in the biot-savart equation.
i have a feeling that since the problem asks for a vector, i need to analyze each wire individually based on their direction, is this a correct assumption?
help appreciated