bdizzle329
- 2
- 0
An electron in a hydrogen atom occupies the combined position and spin state.
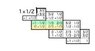
\Psi\left(\vec{r},\xi\right)=\left(\sqrt{1/3}Y^{1}_{0}\xi_{+}+\sqrt{2/3}Y^{1}_{1}\xi_{-}\right)
What are the possible measured values of J^{2} (where J is the total angular momentum of the electron L + S) and with what probability will each be found?
J^{2} = \hbar^{2}j\left(j+1\right)
\left|l-s\right|\geq j \geq l+s , where l and s are the orbital angular momentum and spin angular momentum quantum numbers, respectively.
I know that, according to the given position state of the electron and the fact that it is an electron, l = 1 and s = 1/2.
I know that j will be 1/2 or 3/2. Therefore, J^{2}, when measured, will be either 3/4\hbar^{2} or 15/4\hbar^{2}.
I am having trouble determining the associated probabilities of the possible measurement values for J^{2}. From what I have read about addition of angular momentum, it would seem that I would need to calculate the Clebsch-Gordon coefficients for the total angular momentum. I am not really sure where to start. I have read Griffiths' explanation for angular momentum and the Clebsch-Gordon coefficients but he doesn't explain how to use them for total angular momentum.
I feel dumb asking this kind of question but I am having trouble understanding Quantum Mechanics.
\Psi\left(\vec{r},\xi\right)=\left(\sqrt{1/3}Y^{1}_{0}\xi_{+}+\sqrt{2/3}Y^{1}_{1}\xi_{-}\right)
What are the possible measured values of J^{2} (where J is the total angular momentum of the electron L + S) and with what probability will each be found?
J^{2} = \hbar^{2}j\left(j+1\right)
\left|l-s\right|\geq j \geq l+s , where l and s are the orbital angular momentum and spin angular momentum quantum numbers, respectively.
I know that, according to the given position state of the electron and the fact that it is an electron, l = 1 and s = 1/2.
I know that j will be 1/2 or 3/2. Therefore, J^{2}, when measured, will be either 3/4\hbar^{2} or 15/4\hbar^{2}.
I am having trouble determining the associated probabilities of the possible measurement values for J^{2}. From what I have read about addition of angular momentum, it would seem that I would need to calculate the Clebsch-Gordon coefficients for the total angular momentum. I am not really sure where to start. I have read Griffiths' explanation for angular momentum and the Clebsch-Gordon coefficients but he doesn't explain how to use them for total angular momentum.
I feel dumb asking this kind of question but I am having trouble understanding Quantum Mechanics.