Conducting Rod in Electric Field

[Apteronotus]

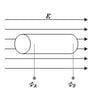
If an uncharged conductor, a metal rod say, is placed in a uniform electric field E, parallel to the field (see figure), does it develop a potential difference between its two ends?

If so, how is the potential difference related to the field E?

 

[kthouz]

If so, how is the potential difference related to the field E?

By the definition, the electric potential, as the energy required to bring a point charge from point B to point A, is given by the negative integral of E over the distance dr from B to A. That is,
\int^{B}_{A}Edr
Just try to apply this on your case where A and B are different positions of the ends.

 

[kcdodd]

Well, if there is a potential difference, it will be very short lived. Since this is a conductor, the charge inside the conductor will re-arrange itself so that there is no potential drop across the conductor.

 

[kthouz]

Well, if there is a potential difference, it will be very short lived. Since this is a conductor, the charge inside the conductor will re-arrange itself so that there is no potential drop across the conductor.

Yes I think you're right! And remember the concept of bound and free charges.

 

[Apteronotus]

Well, if there is a potential difference, it will be very short lived. Since this is a conductor, the charge inside the conductor will re-arrange itself so that there is no potential drop across the conductor.

Actually, I'm not sure this is true. I've given the problem some thought since my original posting. I think a potential difference will in fact develop (and maintain) within the conductor. It's effect will be an electric field within such that the magnitude of the field will be equal to that of the imposed electric field (outside field) and will point in the opposite direction.

So the superposition of the two fields will be zero within the conductor.

 

[kcdodd]

Yes, the field will be zero within the conductor. So, if you do a line integral from one end to the other you will get zero for the potential difference.