Force between two charged hemispheres

[Uku]

Homework Statement

Find the force exerted on the two semispheres by the semispheres of an equally charged hollow sphere.
The charge is q and the radius is R.

Homework Equations

All those that matter.

The Attempt at a Solution

Do I go to polar coordinates and produce a triple integral or do I have some easier alternative?

 

[hikaru1221]

The question is kind of unclear. Does it mean to find the force that one half of an uniformly charged spherical shell exerts on the other half?
Assume so, then working with crazy and tedious calculus is one way. The other way is based on Newton's 3rd law. Calculate the force dF that each surface element dS of charge dQ experiences, then integrate it over one half of the shell for force F. Because of the Newton's 3rd law, the forces of each couple of elements on the same half cancel out. Therefore F is the force needed.

 

[Uku]

Yes, the question is "find the force that one half of an uniformly charged spherical shell exerts on the other half", as you put it better than I did.
I will digest what you said.

Thanks!
U.

 

[granpa]

Is the answer
q/(4R²)

I didnt do any intergal.
I just imagined the sphere as full of massless water under pressure.
(edit:And replace the electric repulsion with gravitational attraction)
I have no idea if it gives the right result though

 

[hikaru1221]

Is the answer
q/(4R²)

No, its dimension is wrong

I didnt do any intergal.
I just imagined the sphere as full of massless water under pressure.
(edit:And replace the electric repulsion with gravitational attraction)
I have no idea if it gives the right result though

Could you elaborate on this? I don't get your idea.

 

[granpa]

gravity and charge follow the same law with just a change in direction.
imagine a planet made of massless liquid.
floating on the top is a scum of mass m spread evenly over the surface.
the pressure at any point is the weight of material above it.
it follows that the pressure is everywhere the same.

split the planet into 2 equal halves with an imaginary plane
the 2 halves are exerting a repulsive force on each other proportional to the pressure and the area of the great circle where they meet.

this repulsive force must be equal and opposite to the attractive gravitational force between the 2 halves or else the configuration would spontaneously change.

surface area of a sphere = 4 great circles

pressure will be proportional to the mass times the surface gravity divided by the surface area
that equals m/R^4 (there's a G in there somewhere)

area of the great circle where the 2 halves meet is proportional is pi*R^2

multiply the 2 together you get m*pi/R^2

 

[hikaru1221]

That's interesting However basically it's the same as doing the integration. The integration hides behind this statement:

the 2 halves are exerting a repulsive force on each other proportional to the pressure and the area of the great circle where they meet.

For this part:

pressure will be proportional to the mass times the surface gravity divided by the surface area

Caution must be taken. This statement is not so true, as gravity at the surface is contributed by the element dm (of area dS) at that position & the rest of the scum. This corresponds to finding the force dF on the element dQ.

Calculations should be done exactly. This problem is tricky at that caution part, so applying proportionality doesn't guarantee a correct answer.

 

[Uku]

Calculate the force dF that each surface element dS of charge dQ experiences
That is the part with the insane integral... If I put myself in perspective of the charge, looking inside the sphere, I have to scan trough all the dS'es contained in $$S=4\pi r^{2}$$, because they all affect me. That is one intense integral.

then integrate it over one half of the shell for force F.
Integrate what? As above, when I am finished scanning with one particle. I just take the adjacent one... another insane integral.

Because of the Newton's 3rd law, the forces of each couple of elements on the same half cancel out.
I agree with this when I think of a section slice. The cosine components cancel.

Basically, could you elaborate on this topic hikaru1221?

 

[granpa]

I see your point now about the 'caution part'.

if the mass is spread out in a perfectly 2d layer of zero width
then the gravity goes from g at the surface to zero in the interior an infinitesimal distance away.
So you take one half.
(just imagine that the width is arbitrarily small but non-zero and imagine how the field changes over the width)
there's a theorem somewhere about that but I can't think of the name of it.

http://en.wikipedia.org/wiki/Heaviside_step_function#Zero_argument

The Heaviside step function, using the half-maximum convention​

 

[Quinzio]

Anyway, this should be the horrible integral$$\frac{q^2}{4\pi^2 R^2}\int_{0}^{2\pi}\int_{0}^{\pi/2} \int_{0}^{2\pi} \int_{0}^{\pi/2} \frac{sin(\phi_A)sin(\phi_B) d\phi_A\ d\theta_A\ d\phi_B\ d\theta_B}{\left [ (cos\phi_A - cos\phi_B)^2 +(sin\phi_Acos\theta_A-sin\phi_Bcos\theta_B)^2 +(sin\phi_Asin\theta_A-sin\phi_Bsin\theta_B)^2 \right ]}$$

The indexes A and B are referred to the hemispheres A and B.
Each hempsphere is swept by a radious in spherical coordinates.

To solve it by hands will require much effort.

 

[hikaru1221]

Calculate the force dF that each surface element dS of charge dQ experiences
That is the part with the insane integral... If I put myself in perspective of the charge, looking inside the sphere, I have to scan trough all the dS'es contained in $$S=4\pi r^{2}$$, because they all affect me. That is one intense integral.

I guess you can find this argument in most classical electrodynamics textbook, but let me introduce it to you (again). No need for an insane integral.

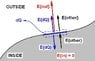
See the attached picture. Here I consider a charge element dQ. Assume that the conductor is in electrostatic equilibrium, then the total E-field outside is $$E_{out}=\sigma / \epsilon_0$$ and the one inside is 0.

Now thanks to the principle of superposition, we can split the total E-field into 2 parts: one due to dQ only $$E_{dQ}$$, the other due to the rest (dQ excluded) $$E_{other}$$.

For $$E_{dQ}$$, it's just like E-field due to an infinite uniformly charged plane. That is because of this assumption: we consider that the width of the charge layer is PHYSICALLY 0, i.e. even if how small dS is, dS is still a lot larger than that width. This assumption is the basic assumption in many continuous charge distribution model; otherwise, we would have to zoom it at the microscopic scale, and deal with a chain of separate electrons and atoms, which is crazy and unnecessarily complicated. Therefore, $$E_{dQ}=\sigma / 2\epsilon_0$$. Notice that $$E_{dQ}$$ has different directions on different side of dQ.

For $$E_{other}$$, we don't have to calculate it now. But one thing we can be sure about is that it is CONTINUOUS at the position of dQ. This is due to an important characteristics of E-field: the E-field due to a distribution of charge is only discontinuous when passing through charges. Here the distribution of charge excludes dQ, and we only consider the E-field due to this distribution (i.e. ignore the existence of dQ), so passing through the position of dQ, there is no charges and thus $$E_{other}$$ is continuous, which corresponds to the unchanged direction of $$E_{other}$$ at the position of dQ.

So from the conclusions about the directions, we have:
OUTSIDE: $$E_{out} = E_{dQ} + E_{other}$$, so: $$E_{other} = E_{out} - E_{dQ} = \sigma / 2\epsilon_0$$
INSIDE: $$E_{in} = E_{dQ} - E_{other}$$, and we can see that the above result $$E_{other} = \sigma / 2\epsilon_0$$ is consistent with the fact that $$E_{in} = 0$$.

We know that the force on dQ is due to E-field of the rest: $$dF = E_{other}dQ$$. So now do you need a crazy integral?

I see your point now about the 'caution part'.

if the mass is spread out in a perfectly 2d layer of zero width
then the gravity goes from g at the surface to zero in the interior an infinitesimal distance away.
So you take one half.
(just imagine that the width is arbitrarily small but non-zero and imagine how the field changes over the width)
there's a theorem somewhere about that but I can't think of the name of it.

http://en.wikipedia.org/wiki/Heaviside_step_function#Zero_argument

The Heaviside step function, using the half-maximum convention​

I don't think this works for gravity (the "changing from g to zero" part), because the gravitational field (magnitude) is the same on both sides of the surface (I'm not sure if I get your point correctly). But this can be applied to the surface charge of a conductor in electrostatic equilibrium. Anyway the argument for taking 1/2 is applicable to both cases.

Applying this argument to my proof above, we don't even need to find $$E_{dQ}$$. We only need to know that due to symmetry of the E-field, $$E_{dQ}$$ has the same magnitude on both sides, and of course, opposite directions (this is also due to symmetry!). Therefore:
$$E_{out} = E_{other} + E_{dQ}$$
$$E_{in} = E_{other} - E_{dQ}$$
Summing the 2 equations side by side, we obtain:

$$E_{other} = \frac{E_{out}+E_{in}}{2}$$

From here, we can deduce the expected result of $$E_{other}$$.@Quinzio: No comment. I don't like dealing with crazily crazy integral. Good luck

 

[granpa]

I don't think this works for gravity (the "changing from g to zero" part), because the gravitational field (magnitude) is the same on both sides of the surface (I'm not sure if I get your point correctly).

the field in the interior of a hollow planet would be zero. Remember that all the mass is in an infinitely thin shell (or scum) on the surface
Thats why I said the liquid was massless.

gravity and charge follow the same law with just a change in direction.
imagine a planet made of massless liquid.
floating on the top is a scum of mass m spread evenly over the surface.[/color]
the pressure at any point is the weight of material above it.
it follows that the pressure is everywhere the same.

split the planet into 2 equal halves with an imaginary plane
the 2 halves are exerting a repulsive force on each other proportional to the pressure and the area of the great circle where they meet.

this repulsive force must be equal and opposite to the attractive gravitational force between the 2 halves or else the configuration would spontaneously change.

 

[hikaru1221]

Ah, okay, I forgot that point. Sorry