Corsan
- 13
- 0
Homework Statement
I have been tasked with finding the angle of twist of the following component:
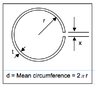
Hollow tube 40mm diameter, 2mm wall thickness, with a 2mm cut along its length (see image), x=2mm.
Homework Equations
Please see attachment for equations.
The Attempt at a Solution
Please see attachment for my attempt.
I calculated this to be 1.70x10-8 radians/metre.
This seems very small (incorrect?).
Can anyone spot any obvious errors with the equations/workings out?
Thanks in advance