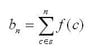bitttttor
- 11
- 0
What does this mean? (see attachment)
"Where b is a block defined by the contiguity condition c that may exist between elements of s, and n is the number of elements in that block"
I know is not possible to get a solution without the actual function, but how does this reads?
"Where b is a block defined by the contiguity condition c that may exist between elements of s, and n is the number of elements in that block"
I know is not possible to get a solution without the actual function, but how does this reads?
Attachments
Last edited: