Proving the Parallelogram Theorem: Sum of Side Squares = Diagonal Squares

[nickadams]

Homework Statement

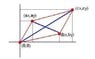
Apply the formula for the distance between two points to prove the well-known theorem: In a parallelogram the sum of the squares of the sides is equal to the sum of the squares of the diagonals.

Homework Equations

It gave a hint saying to put one of the parallelogram's vertices at the origin. Also, it hinted to keep in mind that x-values can only be positive in the 1st and 4th quadrants. It says "upon realizing that, the proof of the theorem reduces to checking a simple algebraic identity. Which?"

Distance formula is √((x1-x2)^2+(y1-y2)^2)

The Attempt at a Solution

Okay what I know about a parallelogram is that its opposite sides are parallel and its opposite angles are equal. What do they mean by "reduces to checking a simple algebraic identity"?

I am lost

 

[ehild]

Draw a picture of a parallelogram. One vertex at the origin, and given the coordinates of two other vertexes, how do you get the coordinates of the fourth vertex?

ehild

 

[nickadams]

Draw a picture of a parallelogram. One vertex at the origin, and given the coordinates of two other vertexes, how do you get the coordinates of the fourth vertex?

ehild

Thanks ehild,

If vertex A is unknown you can use the equations Ax = Cx-Bx and Ay = Cy-By
If vertex B is unknown, use: Bx = Cx-Ax and By = Cy-Ay
If vertex C is unknown, use: Cx = Ax+Bx and Cy = Ay+By

The distance squared to the diagonal from the origin to vertex C is given by Cx^2 + Cy^2

and the distance squared of the other diagonal is given by (Bx-Ax)^2 + (By-Ay)^2

so we have...

Cx^2 + Cy^2 + (Bx-Ax)^2 + (By-Ay)^2 = Ax^2 + Ay^2 + Bx^2 + By^2 + (Cx-Ax)^2 + (Cy-Ay)^2 + (Bx-Cx)^2 + (By-Cy)^2

Since (C-A)^2 = B^2 and (B-C) = A^2 we can replace those on the right side of the equation and simplify it to 2A^2 + 2B^2

now we have to simplify the left side of the equation and we can do that by expanding the (B-A)^2 parts and replacing C with (A+B) and then expanding which will then cause that side to equal 2A^2 + 2B^2 as well. And that is the solution?
I am curious what simple algebraic identity we are checking?

 

[ehild]

Looking at the problem more carefully, it is totally wrong. The sum of the squares of the diagonals is twice the sum of the squares of the sides. It is simpler to derive with vectors. If the origin is one vertex of the parallelogram, \vec{a} and \vec{b} are the two sides. One diagonal is \vec{d_1}=\vec{a}+\vec{b}, the other diagonal is \vec{d_2}=\vec{a}-\vec{b}.

The square of the magnitude of a vector is equal to its scalar product by itself.

d_1^2=\vec{d_1}\cdot \vec{d_1}=(\vec {a}+\vec {b})\cdot(\vec{a}+\vec{b})=\vec a^2+\vec b^2+2\vec a \cdot \vec b

d_2^2=(\vec {a}-\vec {b})\cdot(\vec{a}-\vec{b})=\vec a^2+\vec b^2-2\vec a \cdot \vec b

d_1^2+d_2^2=2 a^2+2 b^2

If you know the law of cosines, the derivation is even more simple. See: http://mathworld.wolfram.com/Parallelogram.html

ehild

 

[NascentOxygen]

Looking at the problem more carefully, it is totally wrong.

No it isn't. You've got yourself confused. Here, you'll need these:

The sum of the squares of the diagonals is twice the sum of the squares of the sides.

Can something be both right and wrong at the same time?

It is simpler to derive with vectors.

Your working is all correct. You just blundered at interpreting the result.

d_1^2+d_2^2=2 a^2+2 b^2

Let's rewrite this in a form that gives a clear reminder that a parallelogram has four sides:
d_1^2+d_2^2=a^2 + a^2+ b^2 +b^2
QED

 

[ehild]

Let's rewrite this in a form that gives a clear reminder that a parallelogram has four sides:
d_1^2+d_2^2=a^2 + a^2+ b^2 +b^2
QED

Ohhh! Of course, there are four sides... That happens when one sees only the formula, without thinking of reality.

And that simple algebraic identity can be that (a+b)²+(a-b)²=2a²+2b².

 

[NascentOxygen]

And that simple algebraic identity can be that (a+b)²+(a-b)²=2a²+2b².

Good, that explains one hint.

Any thoughts on the second?

Also, it hinted to keep in mind that x-values can only be positive in the 1st and 4th quadrants.

 

[ehild]

Do you think I can read the mind of the unknown maker of the problem? I try:

it hinted to keep in mind that x-values can only be positive in the 1st and 4th quadrants. Upon realizing that, the proof of the theorem reduces to checking a simple algebraic identity.

I guess he had Cosine Law in mind. The shorter diagonal d₁ is opposite to the smaller angle, θ <pi/2 in the first or fourth quadrant, and the longer diagonal d₂ is opposite to the angle 180-θ. If a and b are the lengths of the sides, the square of the diagonals are

d_1^2=a^2+b^2-2ab\cos(\theta)
d_2^2=a^2+b^2-2ab\cos(180-\theta)=a^2+b^2+2ab\cos(\theta)

cos(180-θ) =-cos(θ), therefore

d₁²+d₂²=2(a²+b²)

But then I do not know what is the simple algebraic identity. cos(180-θ) =-cos(θ) is simple but it is not algebraic?

ehild

 

[sankalpmittal]

Do you think I can read the mind of the unknown maker of the problem? I try:



I guess he had Cosine Law in mind. The shorter diagonal d₁ is opposite to the smaller angle, θ <pi/2 in the first or fourth quadrant, and the longer diagonal d₂ is opposite to the angle 180-θ. If a and b are the lengths of the sides, the square of the diagonals are

d_1^2=a^2+b^2-2ab\cos(\theta)
d_2^2=a^2+b^2-2ab\cos(180-\theta)=a^2+b^2+2ab\cos(\theta)

cos(180-θ) =-cos(θ), therefore

d₁²+d₂²=2(a²+b²)

But then I do not know what is the simple algebraic identity. cos(180-θ) =-cos(θ) is simple but it is not algebraic?

ehild

Hello ehild !
You don't have to do so much of calculation. Its just simple coordinate geometry.

To OP nickadams :
Draw a parallelogram and and mark the coordinates of four vertex - (a,b) , (c,d) ... (g,h) or such like. Then you just apply the distance formula correctly. You will surely get the way out.

 

[ehild]

Hi sankalpmittal,

nickadams has solved the problem in post #3. Nascent Oxygen and me are trying to find out what the problem maker meant with his hints. By the way, I think applying the Cosine Law is the simplest solution.

ehild

 

[NascentOxygen]

nickadams has solved the problem in post #3. Nascent Oxygen and me are trying to find out what the problem maker meant with his hints.

Yes, a proof was easy enough to come up with. It's using a method that demonstrates intelligent use of the hints that eluded me!

I think you correctly read the examiner's mind.