Where Does the Formula for L_0 in Audio Output Transformers Come From?

[yungman]

I am reading audio output transformers. This is a paragraph from RDH4 and I don't understand where the formula of L_0\; come from. Please see attachment.

 

[uart]

It looks like it's just L = \mu \mu_0 N^2 A/l where \mu_0 \simeq 1.26 E-6 H/m is folded in with the conversion from meters to inches to give the combined constant of 3.2E-8.

 

[yungman]

It looks like it's just L = \mu \mu_0 N^2 A/l where \mu_0 \simeq 1.26 E-6 is folded in with the conversion from meters to inches to give the combined constant of 3.2E-8.

Thanks for the reply. What is the magnetic path l?

L_0=\frac {3.2A\mu N^2}{10^8\times l}

Also where is 3.2EE2 come from. \mu_0\;=1.256EE-6 won't get 3.2EE2.

Thanks

Alsn

 

[uart]

Thanks for the reply. What is the magnetic path l?

L_0=\frac {3.2A\mu N^2}{10^8\times l}

Also where is 3.2EE2 come from. \mu_0\;=1.256EE-6 won't get 3.2EE2.

Thanks

Alsn

No, the geometric factor A/l just has units of length. In SI units you use m^2 and m to give A/l in meters. Then of course you use \mu_0 in H/m (1.26E-6 H/m).

If however you use inches for A/l then you'll need \mu_0 in H/in, so approx divided by 39.4 to give 3.2E-8

 

[yungman]

Thanks, so it's just going from meter to inches.

So what is the path length [itesx]l[/itex]? It was given 4.5 inches, where is this come from? Is this the length of the coil?

 

[uart]

Thanks, so it's just going from meter to inches.

So what is the path length [itesx]l[/itex]? It was given 4.5 inches, where is this come from? Is this the length of the coil?

Yeah, it's the mean flux path length.

 

[yungman]

Thanks Uart, you are of big help.

 

[yungman]

Actually I have another question:

We know for solenoid, B=\mu_0\mu n I\;\hbox{ where n is number of turns per unit length.}

So L=\mu_0\mu n^2 A \;\hbox{ where A is the cross section area of the solenoid.}

The equation in the article, N is the total number of turns in the given length. so:

n=\frac N l\;\Rightarrow\; n^2=\frac {N^2}{l^2}

With that L_0\; should be:

L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l^2}\;\hbox{ instead of }\;L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l}

 

[uart]

With that L_0\; should be:

L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l^2}\;\hbox{ instead of }\;L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l}

No, the equation you post for the solenoid is not for the total inductance, it is for the inductance per unit length. It should read :

\frac{L}{l}=\mu_0\mu n^2 A

 

[yungman]

No, the equation you post for the solenoid is not for the total inductance, it is for the inductance per unit length. It should read :

\frac{L}{l}=\mu_0\mu n^2 A

Thanks, do you go to sleep? I put in my sleeping in between these posts and you're still here!

So basically the total inductance is take the inductance per unit length times the length:

L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l^2} \times l \Rightarrow \; L_0= \frac {3.2A \mu_0\mu}{10^8}\frac{N^2}{l}

 

[yungman]

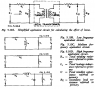
I have a different question, below is the equivalent circuit from the book: The first image is the part in question about the input impedance. The middle picture is the equivalent circuit at different frequency from the book.

The last picture on the right is my equivalent circuit. The top is the equivalent circuit of the real transformer.
(1) is the equivalent circuit refer to the primary.
(2) is the low frequency equivalent.
(3) is the equation of RA using my equivalent circuit which is different from the book in the first image.
(4) is the high frequency equivalent.

As you can see, the way I draw the equivalent circuit is different from the book, I don't think I can agree with the derivation of the book in the first image on the left. Even the equivalent circuit from the book Handbook of Transformer Design and Application by Flanagan and Wikipedia agree with me as in (1) of my drawing:

http://en.wikipedia.org/wiki/Transformer

 

[yungman]

Anyone?