great_sushi
- 30
- 0
I am going to build a drum out of a propane tank. I think it will be handy to find the resonant frequency of the tank and choose the tuning accordingly so not to pick frequencies that are extremely damped.
I have a cavity resonance formula found on hyper physics
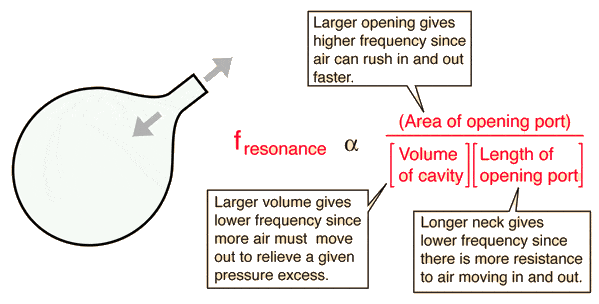
I am not going to build a drum with only one note, there will be approximately 7. 7 notes in most scales. http://muzmaker.ru/uploads/posts/2009-04/1240604374_717ff323216270166.jpg
If you look at the image you'll see the notes, I am going to refer to them as tongues.
Once I find the resonant frequency I can decide on the tuning. Another problem is choosing the dimensions of the tongues at the top. I've been trying to find another formula so that I can determine the size of the tongues, so a larger tongue results in a slower oscillation producing a lower note and vice versa. But I will need to relate the tongue dimensions to the resonant frequency of the tank.
Im curious to know how to calculate the resonant frequency of something steel with particular dimensions.
Once I have that relation I can move forward. Also, fine tuning will be done by either bending the tongue downward/upward permanently as to result in a lower/higher frequency respectively.
Thankyou, If all goes well, my drummer sister will have another present for christmas.
I have a cavity resonance formula found on hyper physics
I am not going to build a drum with only one note, there will be approximately 7. 7 notes in most scales. http://muzmaker.ru/uploads/posts/2009-04/1240604374_717ff323216270166.jpg
If you look at the image you'll see the notes, I am going to refer to them as tongues.
Once I find the resonant frequency I can decide on the tuning. Another problem is choosing the dimensions of the tongues at the top. I've been trying to find another formula so that I can determine the size of the tongues, so a larger tongue results in a slower oscillation producing a lower note and vice versa. But I will need to relate the tongue dimensions to the resonant frequency of the tank.
Im curious to know how to calculate the resonant frequency of something steel with particular dimensions.
Once I have that relation I can move forward. Also, fine tuning will be done by either bending the tongue downward/upward permanently as to result in a lower/higher frequency respectively.
Thankyou, If all goes well, my drummer sister will have another present for christmas.